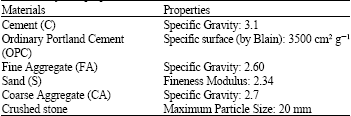
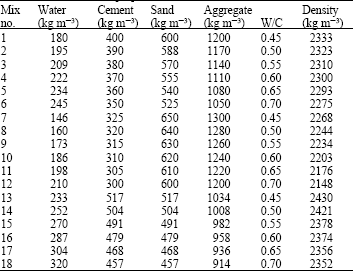
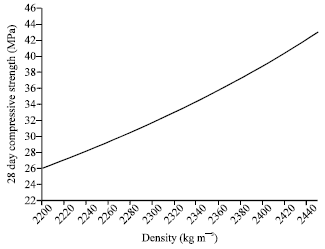
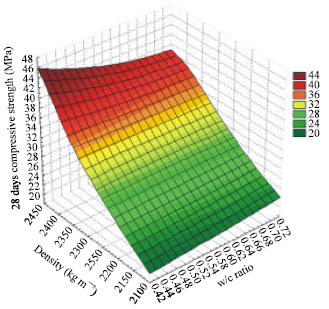
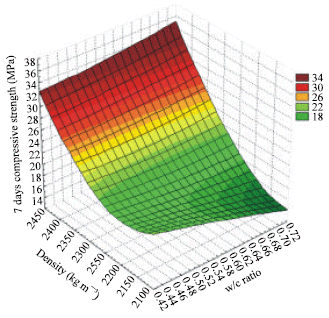
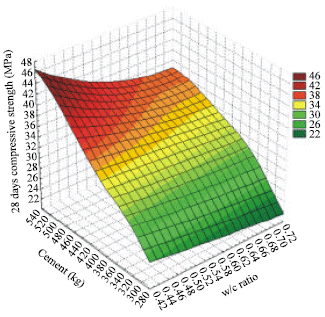
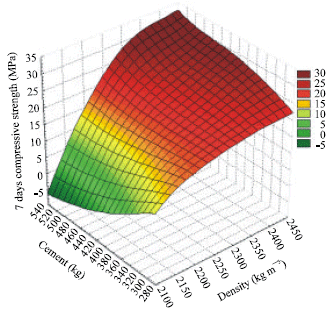
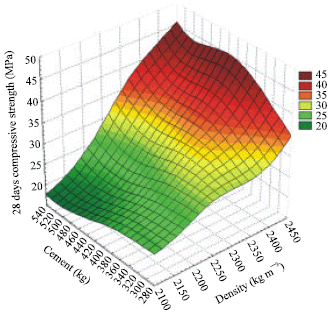
Research Article
Potential for Utilising Concrete Mix Properties to Predict Strength at Different Ages
Faculty of Engineering and Built Environment, National University of Malaysia UKM, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia
Suhad M. Abd
Faculty of Engineering and Built Environment, National University of Malaysia UKM, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia
Roszilah Hamid
Faculty of Engineering and Built Environment, National University of Malaysia UKM, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia
M. Jamil
Faculty of Engineering and Built Environment, National University of Malaysia UKM, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia