Review Article
Deign of Photovoltaic Water Pumping Systems at Minimum Cost for Palestine: A Review
Department of Electrical Engineering, Palestine Technical University-Kadoorie, Tulkarm, Palestine
Geographically, Palestine is located between latitudes 34.15° and 35.40° East and between the latitude circles 29.30° and 33.15° North. The sun has a daily average sunlight about 8 hours throughout the year. The daytime temperatures ranging from 14° to 26°C are benign to the operation of the standalone photovoltaic (SPV) system where the average solar irradiation is 5.5 KWh m-2. Due to rich solar irradiation and mild ambient temperatures, the SPV system is considered as one of the most promising applications of renewable energy sources to supply power for the remote areas in Palestine (Mahmoud and Ibrik, 2003).
Recently the water demanding has been increased due to the increasing in the population and the availability of water has become more crucial than ever before. A source of energy to pump water is also a big problem in many developing countries. Developing a grid system is often too expensive because rural villages are frequently located too far away from existing grid lines, also depending on an imported fuel supply is difficult and risky; foreign exchange rates fluctuate and the economy of many developing countries can then plummet. Even if fuel is available within the country, transporting that fuel to remote, rural villages can be difficult. There are no roads or supporting infrastructure in many remote villages. The use of renewable energy is attractive for water pumping applications in rural areas of many developing countries. Transportation of renewable energy systems, such as photovoltaic (PV) pumps, is much easier than other types because they can be transported in pieces and reassembled on site (Khatib, 2010).
Water pumping systems classified depending on the kind of the used pump (AC or DC) and the configuration of the systems. There are two configurations of the water pumping systems; standalone systems and hybrid systems. Hybrid systems in general used two energy source like wind turbine or diesel generator or PV. The AC standalone water pumping systems in general consist of PV array, inverter with centralized maximum power point tracker and pump. Such as mentioned system can be with a block of batteries as a backup power supply, but since the system cost is very important factor, the systems sometimes designed in a way to meet the village demand during the solar day without any needs for batteries (Boyle, 2004).
The advantages of PV powered pumps are low maintenance, no pollution, easy installation, reliability, possibility of unattended operation and capability to be matched to demand. The disadvantages are the high initial cost and the variable water production. If a reliable pump system is to be realized, the system designer must be familiar with the well, the storage system, the terrain surrounding the well and manufacturers’ data on available pumps (Boyle, 2004).
In this study a review of design, installing and evaluating photovoltaic water pumping systems will be introduced. Moreover, a designing example will be provided so as to highlight the optimum designing steps.
PUMPS CHARACTERISTICS
There are two broad categories of pumps being used in stand-alone PV systems around the world rotating and positive displacement and there are many variations on the designs of these two basic types. Examples of the rotating pump type are centrifugal, rotating vane, or screw drive. These pumps move water continuously when power is presented to the pump. The output of these pumps is dependent on head, solar radiation (current produced) and operating voltage. They are well suited for pumping from shallow reservoirs or cisterns. They can be tied directly to the PV array output but their performance will be improved by using an electronic controller such as a linear current booster to improve the match between the pump and PV array. Positive displacement pumps move packets of water. Examples are diaphram pumps and piston pumps (jack pumps). These are typically used for pumping water from deep wells. Their output is nearly independent of head and proportional to solar radiation. Jack pumps should not be connected directly to a PV array output because of the large load current changes during each pump cycle (Chowdhury et al., 1993).
Peak power controllers are recommended. The controllers adjust the operating point of the PV array to provide maximum current for motor starting and then keep the array operating at the maximum power conditions some system designers use batteries between the jack pump and the array to provide a stable voltage source to start and operate the pump (Khatib et al., 2010a).
Usually they are not sized to provide nighttime pumping, but only to give stable system operation. Pumps are also categorized as surface or submersible. Surface pumps have the obvious advantage of being more accessible for maintenance. When specifying a surface pump you must distinguish between suction and lift. A pump may be installed a few feet above the water level, with a pipe from the pump to the water. The maximum length of the pipe is determined by the suction capability of the pump. The pump may then lift the water to a storage tank above the pump. The elevation of the storage tank is determined by the lift capability of the pump. Most submersible pumps have high lift capability. They are sensitive to dirt sand in the water and should not be run if the water level drops below the pump. The type of pump will depend on the water required, the total dynamic head and the capability of the water source. Both rotating and displacement pumps can be driven by ac and dc motors. The choice of motor depends on water volume needed, efficiency, price, reliability and availability of support. DC motors are an attractive option because of their compatibility with the power source and because their efficiency is usually higher than that of ac motors. However, their initial cost is higher, the selection may be limited in some countries and the brush type motor requires periodic maintenance. Some brushless dc motors are available and promise improved reliability and decreased maintenance. AC motors require a dc to ac inverter, but their lower price and wider availability are advantages (Chowdhury et al., 1993).
In water pumping systems, storage can be achieved by using batteries or by storing the water in tanks. Adding batteries to a system increases cost and decreases reliability. Water storage is better for most applications. However, considerable evaporation losses can occur if the water is stored in open tanks or reservoirs. Closed tanks large enough to store several days water supply can be expensive. In some countries, these tanks are not available or the equipment necessary to handle, move and install the tanks may not be available. Also, any water storage is susceptible to vandalism and pollution (Weiner and Levinson, 1996).
DESIGN OF THE SYSTEM
The first requirement is an estimate of the water needed and the amount of water that can be supplied by the source (flow rate). If the water needs vary throughout the year, a monthly profile should be drawn and matched to a monthly profile of the production capability of the water source. It is important to know the worst case conditions, so data on production and demand for the driest months of the year should be available or estimated. If the capability of the water source is limited, the designer must take action. One thing that can be done is to improve the water source or develop other sources. Using a smaller pump is another option but the availability of different size pumps is limited. Another method is to incorporate batteries into the system and distribute the pumping time over a longer period. This is one of two reasons to use batteries in a water pumping system. The other is if the pumping time needs to be controlled--usually to pump at a high flow rate for a short time. An example might be a residential system with storage tanks when you want to pump all the water for the household during times when other loads are not operating. Although using batteries in a system will maximize the pump efficiency--because of the steady operating conditions presented to the pump and motor--most water pumping systems do not contain batteries. It is usually less expensive to store water than to store electricity. If a tank is available, the system can pump all day and the water stored for later use. Gravity-feed or a small pressure pump can then be used to deliver the water to the user (Weiner and Levinson, 1996).
Another variable that must be the specified is the pumping time factor. This time factor is referenced to the number of daily peak sun and hours. If a direct-drive centrifugal pump is used, the pumping time factor will equal 1.0. In other words, the pump will operate with varying efficiency through all daylight hours but that is equivalent to operating at the rated efficiency during the peak sun hours. If batteries are used, the pumping time factor would be equal to the hours of scheduled operation divided by the number of peak sun hours. If a linear current booster or peak power tracking controller is used between the array and the pump in a direct drive system, the pumping time factor should be 1.2. This takes into account the improvement in pump performance that these devices achieve (Dunlop, 1988).
The pump size, operating time and total power demand can be calculated if the efficiency of the pump and the depth of the water are known. The efficiency of specific pumps depends on pump type and operating conditions. For centrifugal pumps the efficiency is a function of head, flow and solar insulation, all of which will vary throughout the day. Under some conditions the average daily efficiency, called wire-to-water efficiency, can be as little as one-third the peak pump efficiency. In contrast, the efficiency of a displacement pump changes little with changing solar conditions. Some typical wire-to water efficiencies are given in Table 1 (Dunlop, 1988).
Many pumping systems use PV arrays mounted on one-axis trackers. Tracking the array not only increases the hours of operation (peak sun hours) but also provides a more consistent operating point (voltage and current) for the pump motor. Therefore, tracking is recommended for latitudes less than 40° (Khatib et al., 2010b).
System’s sizing: The two most important factors in the operation of a PV pump are the availability of sufficient solar radiation to enable the pump to start (until the solar radiation reaches the threshold level) and the non-linear relationship between the pumping rate and solar radiation. The threshold level of a PV pump depends on the system components. Figure 1 illustrates a schematic diagram of typical PV pump components. It consists of a PV array, an inverter, the motor-pump subsystem and the water tank (German Solar Energy Society (DGS), 2005).
Figure 2 shows the key factors required for any PV water pumping system which are water source capacity, water volume required per day, solar insulation availability, pumping time, static water level, drawdown level, discharge head, pipe size friction, pumping subsystem efficiency. The most important is Total Dynamic Head (TDH) which is the sum of the static head, the drawdown and the equivalent head caused by friction losses in the pipe. TDH is expressed in feet or meters and is dependent on the flow rate (Bucher, 1991).
PV pump components have to be selected carefully for a proper matching of the system. Unlike conventional pumping systems, PV pumps have to be designed and installed properly to be competitive with other pumping technologies.
| Table 1: | Measurement of wire to wire efficiency |
 | |
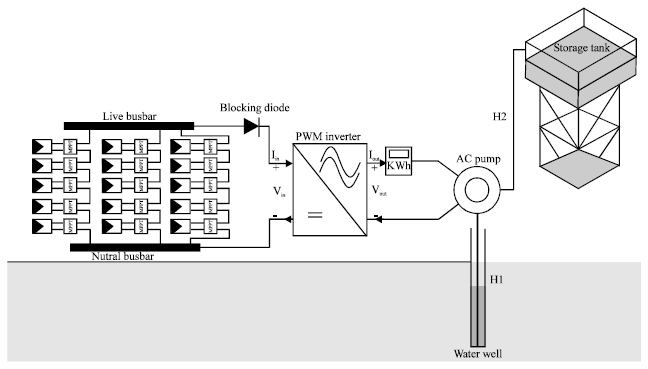 | |
| Fig. 1: | A schematic diagram of typical PV pump components |
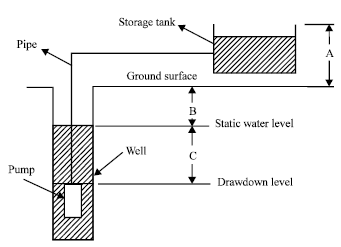 | |
| Fig. 2: | Water pumping system terms |
Each component of a PV pump has intrinsic characteristics affecting the overall operating conditions. Therefore, it is desirable that the intercept of all respective component characteristics follows the maximum power line of the PV array generator. Depending on this internal matching, the efficiency of the overall system and related performances will meet an acceptable range. System design, particularly the PV array capacity, should be reviewed to ensure that sufficient energy is produced to start the motor as early in the day as possible. In principle, modeling components individually and combining them into a single system can optimize PV pumps. This approach could be the most accurate method to maximize the efficiency of each component and, ultimately, the overall system efficiency. This method requires an understanding of each component. Detailed information, such as the ideality factor, the operating principles of diodes, the shunt and series resistance, etc., is not easily ascertained from catalogues. To use this approach, one must know the basic functions of diodes, inverters, motors and pumps. Another simple, fairly accurate design method is to create a clear mathematical relationship between the solar radiation energy, the PV array power and the required hydraulic energy to fulfill the water demand. This method can easily be used by field technicians or by end users. The mathematical relationship between the PV array power and solar radiation energy is (Appelbaum, 1996; Hsiao and Blevins, 1984):
| (1) |
where P is the PV array power (in Watt-peak, Wp), ηr is the efficiency of the PV array at reference temperature (Tr = 25 C), Gr is the solar radiation at reference temperature (Gr = 1000 W m-2) and Apv is the effective area of the PV array, in m2 (Apv = npnsA, where A is the area of a single module and ns is the number of the group of PV cells connected in series each containing np strings in parallel). Equation 1 can be rewritten as (German Solar Energy Society (DGS), 2005):
| (2) |
The effective PV array area is calculated from the relationships of the daily energy output Eε and the daily hydraulic energy Eh (both in kWh):
| (3) |
and
| (4) |
where ηpv is the efficiency of the PV array under operating conditions, GT is the daily solar radiation on the PV array surface (kWh m-2), V is the daily amount of water required m3), h is the total pumping head (m), ηs is the subsystem efficiency, ρ is the density of water and g is the acceleration due to gravity. The efficiency of the PV array is determined from:
| (5) |
where, fm is the matching factor, that is, the ratio of the power output of the PV array under operating conditions to its power output at the maximum power point. The generally accepted value for designing a PV system is fm≈0.90. The value α is the cell temperature coefficient and is from 0.2 to 0.6%/C (0.004 to 0.005/C for Si) and TC is the daily average cell temperature (in C). Cell temperature is dependent on solar radiation, ambient temperature and wind speed. Many researchers have tried to develop a relationship that includes solar radiation, ambient temperature and wind speed through an experimental method. The experimental relation developed by Risser and Fuentes (1983), from Sandia National Laboratories, is a linear relationship of solar radiation, ambient temperature and wind speed. The relation is in the form:
| (6) |
where, Tc and Ta are in C, GT is in W/m2 and the wind speed Ws is in m sec-1.
The simplified cell temperature model that was commonly adopted by many researchers is the relation that includes solar radiation and ambient temperature. The relation is of the form:
| (7) |
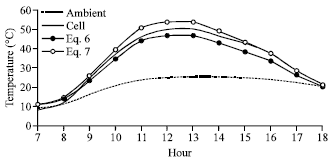 | |
| Fig. 3: | An example of deviation between the measured and calculated values of the monthly average hourly cell temperature |
where Ta is the hourly ambient temperature, NOCT is the module junction temperature under normal operating temperature (G = 800 W/m2, Ta = 20 C and at 1 m sec-1 wind speed). For a wind speed over 1 m s-1, the cell (module) temperature will be lower and the cell temperature decreases as the wind speed increases. Field data were used to compare Eq. 6 and 7; this is presented in Fig. 3 to show the variation of these models from actual field data. From the graph, Eq. 6 tends to be lower than the actual field data, while Eq. 7 tends to estimate higher temperatures than the actual reading at peak hours. However, the deviation of both equations from the actual field data is minimal and both equations can be used to estimate cell temperature.
Once the efficiency of the PV array is determined from Eq. 5, the PV array area can be calculated from Eq. 3 and 4. Thus:
| (8) |
Substituting Eq. 8 into Eq. 2, the PV array size in terms of hydraulic energy and solar radiation energy will be:
| (9) |
From Eq. 9, it is possible to determine the required size of the PV array for a given pumping head and daily water demand, or conversely, to estimate the daily amount of water produced for the given array size and solar radiation energy.
The overall efficiency of a PV pump can be determined from the hydraulic energy and from the solar radiation energy input Pin. That is:
| (10) |
A simple nomogram can be developed using these relationships (Eq. 1 to 9) at various ambient air temperatures. The nomogram shown in Fig. 4 was developed for ambient air temperature Ta of 25°C. This nomogram can be used either to determine the size of a PV array required for the desired pumping head and water demand, or conversely, to estimate the daily amount of water production for a given PV array size and pumping head. If the hydraulic energy varies from month to month as a result of variation in water levels or water demand, the nomogram should be used for each month of the year with the corresponding solar radiation and hydraulic energy. The month with the worst-case combination of solar radiation energy and water demand is usually the design month. To use this nomogram, first determine the water demand from the size of population to be served and the total pumping head. Then draw a line counterclockwise on the nomogram, using the appropriate values of the subsystem’s efficiency and the average daily solar radiation, to get the required array size. Alternately, start clockwise from a known PV array size to obtain the amount of water produced for a given total pumping head (Luque and Hegedus, 2003).
INSTALLATION OF THE SYSTEM
Many failures of PV pumping systems are caused by pump problems. The PV power supply has much higher reliability than the pump/motor subsystem. A good installation of the pumping hardware will increase reliability. Some things to watch for are described below:
Varying water levels: The water level in a well may vary seasonally, daily, or even hourly. The water level in some wells in rocky areas has been reported to drop as much as 75 feet during pumping. The pump must be mounted to keep the water inlet below the water level at all times. If the replenishment rate of a well is lower than the maximum possible pumping rate, a level switch or mechanical valve should be included to protect the pump from operating dry. Float switches should be used on storage tanks if the volume of the tank is smaller than the daily pump rate. This will prevent wasted water or worse, pump damage due to overheating.
Protect the pump input: Sand is a primary cause of pump failure. If the well is located where dirt and sand may be pulled into the pump, a sand screen should be used. Most pump manufacturers offer this option or they can recommend methods for limiting the risk.
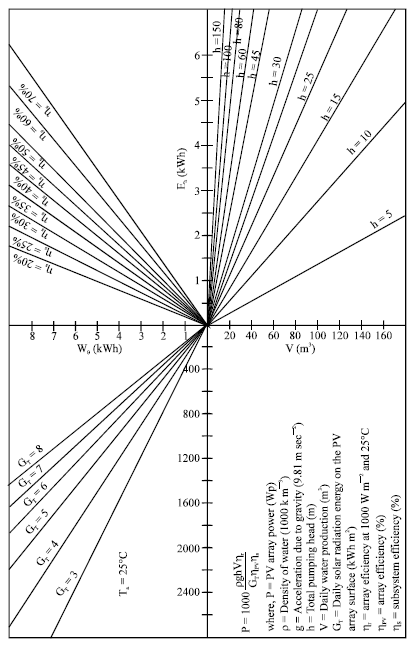 | |
| Fig. 4: | Nomogram used to estimate the size of a PV array and daily water production |
Ground the equipment: Water pumps attract lightning because of the excellent ground they provide. If possible, do not locate the pump system on high ground. Consider erecting lightning rods on higher terrain around the pump. Ground the pump motor, the array frame, all equipment boxes and one system conductor to the well casing (if metal) or to a bare conductor running down to the water level. Never use the pipe string to the pump as a ground, because the ground would be interrupted when maintenance was being performed. Use of movistors to protect electronics is recommended in areas prone to lightning.
Avoid long pipe runs: Friction be used in a well with a jack pump. losses can significantly increase They are lighter than metal, buoythe head and thus the size of the PV ant and much easier to pull for array. Friction losses depend on pump maintenance. The pipe dithe size of the pipe, the length, the ameter should be larger than the flow rate and the number of bends pump cylinder. This will allow the in the pipe. Because the output of a stand-alone PV system is power limited and varies throughout the day, it is particularly important to keep friction losses low. Pump system efficiency can drop to near zero if a large friction loss must be overcome. Try to limit the friction loss to less than 10% of the head. This can be done by oversizing the pipe, eliminating bends and junctions and reducing flow rate. Data on pipe size and friction rates are available from pump manufacturers. pump leathers to be changed by pulling the sucker rod without pulling the pipe.
Protect the control equipment: All electronic control equipment should be housed in weather resistant boxes. All wires should be approved for outdoor use or installed in conduit. Any cables used for submersible pumps should be appropriate for that application. Pump manufacturers will give recommended wire types for their equipment.
Use steel pipe: Steel pipe is recommended for use in the well, particularly if submersible pumps are used. Plastic pipe may break. However, plastic pipe provides an inexpensive way to run water from the well to the storage tank or end user. Fiberglass sucker rods may
Protect the well: Use sanitary well seals for all wells. Bury pipes from wellhead to tank at a depth that will insure the pipe will not be broken by traffic or during future trenching or excavation. Mark pipe runs for future reference (Shrestha and Goel, 2003).
Design consideration of water tanks: Some of the most important factors to consider in designing water tanks follow:
The power source type: The size of the water tank should be greater for PV- and/or wind powered water pumping systems than for conventional systems because of the intermittent nature of the power source. Poor solar radiation or windless days create a significant problem in fulfilling the daily water demand. The size of water tanks for conventional systems depends only on the peak and average daily water demands. However, in the case of PV and wind pumps, the size of water tanks depends on those factors and local weather conditions.
The geographical location of the system: Geographical location is very important for a PV/wind pumping system. Sunny and/or windy areas make PV/wind pumps much cheaper and their use ideal in certain locations. Similarly, the size of water tanks can be smaller in such locations. On the other hand, the size of water tanks should be much larger for areas of low solar radiation or low wind conditions.
The type of end users: Unlike those in urban areas, PV/wind pumps installed in rural communities are often designed based on minimum water demand requirements.
The type of application: Water reservoirs designed for irrigation purposes should be very large compared to those for other water supply purposes. Water reservoirs designed for cattle watering and community use typically depend on per capita water consumption. As a rule of thumb, there should be three days of storage for community water supply and five days of storage for cattle watering.
The size of the water distribution networks: Because it can hold a huge amount of water, large water distribution systems also act as water reservoirs. Small distribution networks with water service at only a few points do not have such option. Many of these services are in rural villages where distribution pipes are usually small. In such cases, it is essential to pump water to holding tanks and then on to distribution networks.
Availability of other water resources: Large tanks may be unnecessary if there is a great amount of annual rainfall in the area. Rainwater can be collected and used for cattle watering and for washing clothes in rural areas. Surface water that flows year round (such as a river) can also provide such services to reduce the need for large capacity water tanks. Unlike conventional pumping systems, estimating the proper size of a PV/wind pumping system, including the water tank, requires a detailed evaluation of each component and the system as a whole. As water tanks often cost less than a PV array or wind machine, installing a larger water tank (instead of a larger PV/wind pumping system) allows for the possibility of storing water for low solar radiation or less windy days. Every means for reducing costs must be considered when designing PV/wind pumping systems. For example, for PV pumping systems, using seasonally adjustable tilt angles can increase the daily water production by 5-10%. It is also necessary to supply enough water for poor solar-radiation or less windy days and to use the surplus water produced on days with optimum sun or wind. Consecutive days with poor solar radiation and little wind are especially difficult when trying to meet daily water demand, but can be offset with the surplus (Hamidat, 1999).
Water tanks for conventional supply systems are designed to hold 30-40% of the total daily water demand. The bare minimum tank size for any community can be estimated by simulating typical one-year daily weather data and estimating the water balance from daily water demand and production over the year. The water balance is the difference between the daily water production and water demand. Negative water balance demonstrates the extra amount of water required over the day. The worst consecutive days of poor solar radiation conditions or little wind are reflected on the values of the water balance. The extra amount of water required for these consecutively poor days is calculated by adding the daily water balance of those days with the negative sign that is equal to the amount of extra stored water required to meet the water demand. Since there may be several consecutive poor days, those days with the largest water requirement is exactly the minimum size of the water tank required to fulfill the community’s water demand. In case of hybrid systems, water tanks can be sized like conventional systems because there is a good possibility of getting enough energy to pump water either from wind, sun, or a standby diesel system (Hamidat, 1999).
Load matching evaluation technique: This section discusses the load-matching factor to evaluate the performance of PV water pumps. This approach has been the most effective and simplest in analyzing the performance of heat collectors during the past few decades. The same approach can be adapted for PV systems’ performance evaluation. The load-matching factor is the ratio of energy acquired by the hydraulic load to the maximum PV array power extracted in a one-day period. This could be stated as the ratio of the power that the PV array delivers to the motor-pump subsystem during the day to the maximum electrical power that can be obtained from the array throughout the day. This can also be defined as the ratio of the actual array output used for water pumping to the array output capability. Thus:
This parameter is very useful for assessing how much of a PV array's real power production capability is being used.
The load-matching factor can be determined from theoretical models or from field experimental data (from solar radiation and PV array power output data). Theoretically, the load-matching factor is expressed as:
| (11) |
where, P is the PV array power output and Ph is the power acquired by the hydraulic load.
The load-matching factor can also be determined graphically from experimental data. Figure 5 represents the typical daily average, hourly PV array power output curve. The horizontal line (CD) shows the threshold level of the electrical load on the PV pump. If we take a short time interval (the shaded areas A and B), the total array output capability can be obtained by integrating over a given time. The actual array output used for pumping is then the area of the curve above the threshold line. The area below the threshold line is the power wasted due to friction and other losses.
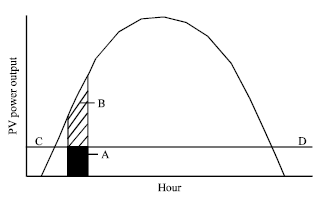 | |
| Fig. 5: | A typical daily average hourly PV array power output |
Therefore, the load matching factor is the ratio of the curve area above the threshold line to the total area of the curve.
Similarly, the load-matching factor can be determined from the daily average, hourly solar radiation curve. Since the PV array power output depends on the distribution of solar radiation, the solar radiation curve over the day will have a similar shape to Fig. 5 and the load-matching factor from the solar radiation curve is defined by:
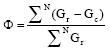 | (12) |
where, N is the number of daily hour readings, GC is the critical solar radiation (or the threshold) to start water pumping and GT is the solar radiation on the tilted surface of the PV array.
Experimental field data are taken to illustrate how the load-matching factor of a PV pump is estimated. These data were taken from a PV pump. From the data, the solar radiation, PV array power and the water output were plotted in one graph, as shown in Fig. 6. In principle, the PV array DC power curve should follow a similar pattern to the solar radiation curve between 8:00 to 9:00 am, but in this case, trees were shadowing part of the array. At the experiment site, the critical (threshold) solar radiation energy required to start pumping water from the graph is 68 W m-2 in the morning and 170 W m-2 in the afternoon. The critical PV array DC power required from the graph is 112 W. In principle, the critical PV power required to start pumping water should always be constant because the threshold power depends on the system components. Because the efficiency of the PV array decreases at higher cell temperatures, the critical solar radiation energy varies over the day, depending on the cell temperature and wind speed of the area. Higher solar radiation energy is required to produce the same amount of DC power at higher cell temperatures.
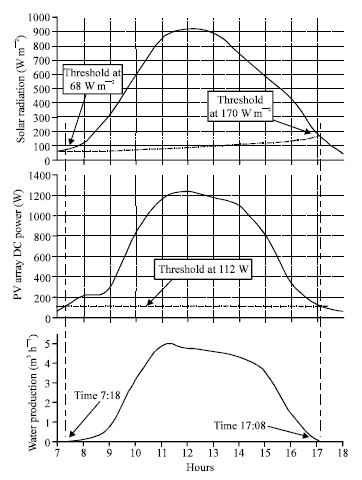 | |
| Fig. 6: | An example of monthly average daily solar radiation energy, DC power output and water production of a PV pump |
On the other hand, higher winds will have a cooling effect on the array. Thus, to produce 112 W of DC power, the PV array requires solar radiation energy of 68 W m-2 in the morning, or 170 W m-2 in the afternoon, respectively. The critical solar radiation can vary from day to day, depending on the weather conditions (temperature, wind speed and other factors). The critical points were found graphically by drawing vertical lines from the beginning and ending points of the water output curve (Chaurey et al., 1992).
The load-matching factor is usually easier to estimate from the PV array power output than from the solar radiation curve. This is because the critical PV array power output is constant, unlike the critical line on the solar radiation curve, which may not be a straight line. The optimum load-matching factor of this PV pump, estimated from the power output curve, is 0.84. This factor could be a bit higher if the trees did not shadow the PV array. This figure is still quite high and shows that the system components are well matched, or properly configured. The threshold line shifts up or down, depending on the type of motor-pump subsystem, capacity and weather conditions. Optimum load matching of PV water pumping systems mainly depends on solar radiation and load profiles. Because the load-matching factor is the ratio of the curve's area above the threshold line to the total area of the curve, the loadmatching factor for a given PV pump is higher on good solar radiation days than during low solar radiation days. Therefore, the load-matching factor varies from season to season. To maximize the performance of a PV water pumping system, the operation of the load line must be close to the maximum PV array power line throughout the day. Thus, because the loadmatching factor is a measure of design quality of the system within the local environment, it has to be as high as possible for all seasons. It is also possible to achieve a higher loadmatching factor by carefully selecting the proper size of PV array and the motor-pump subsystem at the best solar radiation locations. The load-matching factor can be close to unity for a well-matched PV pumping system on the best solar radiation day (Koner, 1995).
The simplest method of measuring a PV pump's performance is to take daily readings of the solar radiation on the PV array's plane, the daily volume of water pumped and the static head of the well. This allows the hydraulic energy to be calculated and then the system efficiency can be estimated at different solar radiation energy levels. Appendix D is an example of a simplified daily PV pump recording form for this purpose (Fiaschi et al., 2005).
Design example: Rural electric cooperatives in Nablus are beginning to supply PV power to their customers who need to pump water for livestock. The conventional method of service was to extend the grid line to the isolated well-even though the income from the customer could never pay for the maintenance of the line, let alone provide a return on the original investment. As these remote lines require replacement, either because of age or storm damage, a number of utilities have discovered that a PV pumping system can be provided for the customer at a fraction of the cost of replacing the line. This example is of a rancher in Nablus that requires about 500 gallons of water per day for 40 cows. The pasture where the well is located is used in wintertime only. There is a 2,500 gallon tank near the well that provides water (gravity fed) to smaller water tanks distributed throughout the pasture. The load is critical as the cattle cannot go without water more than one day in winter, this small pump uses a 12 volt dc two stage diaphragm pump and is designed to pump over 500 gallon per day (2,000 L day-1) from a level of 20 m. The water level in this well is only 10 m with a maximum drawdown of 6 meters. A float switch in the main watering tank controls operation of the pump.
The solar potential in nablus: A real solar irradiation data has been taken from the Energy Research Center, An-Najah National University for Nablus region. The Average solar irradiation is 5.5 KWh m-2-day where the minimum solar irradiation (2.79 KWh m-2-day) is in January and December. The maximum value of the solar irradiation was in June which is 8.74 KWh m-2-day. Table 2 shows the average of solar irradiation during the same year.
Key design information:
| • | Application: Livestock Watering |
| • | Site: Nablus, Palestine |
| • | Location/Elevation: 32° 11′ 31.7° N, 35° 22′ 16.11° E |
| • | Temperature range (C°): 14 - 26 |
| • | Availability required: Critical |
| • | Dynamic head (m): 17 |
| • | Water required/day: 2000 liter October to March |
PV system size: Calculate the water pumping load: the Pumping rate (L/hour) can be given by:
| (13) |
Using Eq. 13 and supposing that the Pumping Time factor (1.2) then the system must pump 243 L h-1.
The array Energy (Wh day-1) can be calculated by:
| (14) |
| Table 2: | Monthly-daily average solar irradiation |
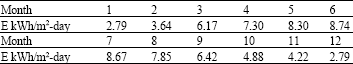 | |
| Station: Nablus monthly-daily average year: 2009 | |
Using Eq. 14 the hydraulic Energy is 93 Wh day-1. Then the Array energy is given by the following:
| (15) |
The energy of the PV modules array is 372 Wh day-1.
Suppose that the system’s nominal voltage is 12 V then the ampere hour load is 31 Ah day-1.
As for the design current and based on the PSH for Palestine, the worst months are January and December which both are 2.97 (KWh m-2-day), then the design current is the load current divided by the worst PSH which is 10.5 A.
Calculate the system’s PV array size: Suppose that the PV module’s rated current and voltage are 3 A, 15.9 V, respectively then the number of PV modules in parallel is the design current divided by the PV module’s rated current which is equal to 3 PV modules. One PV module needed in series since the system’s nominal voltage is 12 V.
Pumping rate: Based on the calculated size of the PV system, the Pumping rate (L day-1) is given by:
| (16) |
Where, Np is the number of modules in parallel, Im is the modules current, Vnominal the system nominal voltage, PSH is the peak sun shine and TDH is the total dynamic head. Using Eq. 16 the pumped water per day is 3206 (L day-1) or 486 (L h-1).
Figure 7 shows a schematic diagram of the designed system.
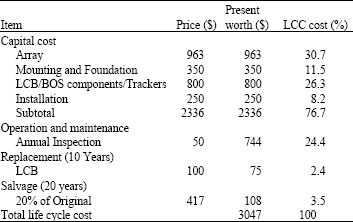
Economic analysis of the designed system: Table 3 shows an economic analysis of the designed system using the present worth method.
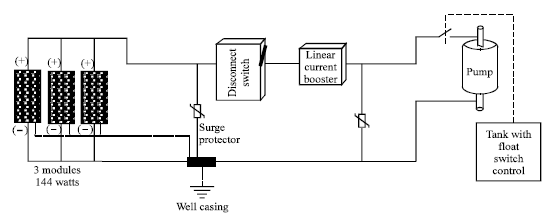 | |
| Fig. 7: | Schematic diagram of the designed system |
| Table 3: | Economic analysis |
 | |
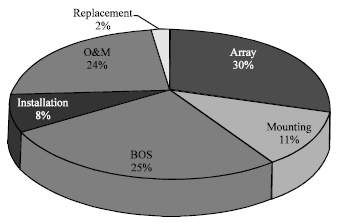 | |
| Fig. 8: | System's element cost |
Figure 8 shows the cost element as percent of LCC.
A review of designing PV water pumping systems for Palestine has been introduced. Besides that an installation and evaluation guide has been introduced for these systems so as to improve its reliability and feasibility. A designing example has been provided in order to show an optimum design for PV water pumping systems. Based on the design example and the real sun irradiation data, the sun irradiation average for Palestine is 5.5 kWh m-2 and the PV panels should be tilted at () to the north. Adding maximum power point tracker and sun tracker increases the efficiency of the system.
The author would like to thank Dr. Imad Ibrik, the director of the Energy research center, An-Najah National University, Nablus, Palestine for providing him real data about the sun irradiation for Palestine.
Mahmoud Reply
i am doing my master in this PV Pumping
Tamer Khatib
That is great. feel free to if you have any inquiry in this regards