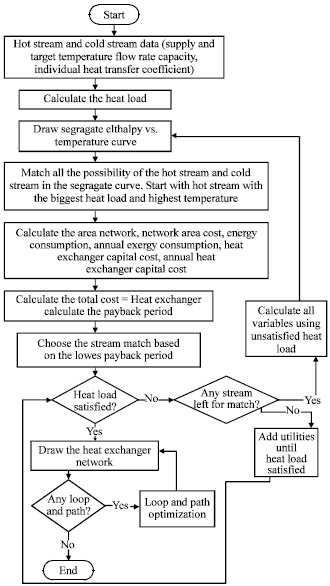
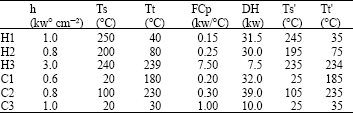
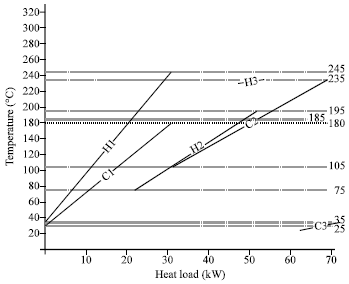
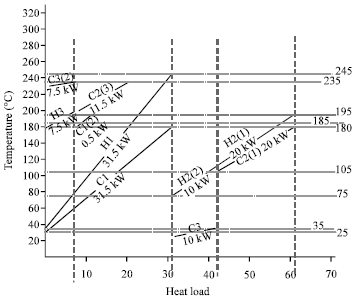
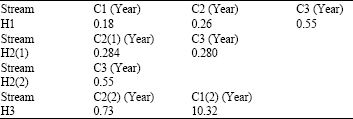
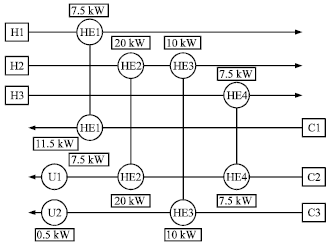
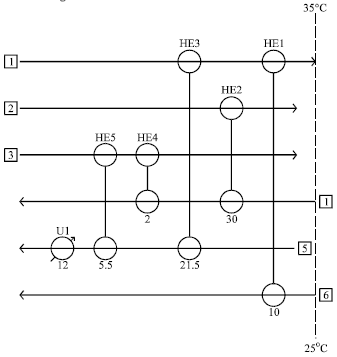
Research Article
A New Systematic Method for Optimal Heat Recovery Networks Design with Minimum Area and Exergy Loss
Process System Engineering Centre, University Technology Malaysia, UTM Skudai, Johor, Malysia
S.R. Wan Alwi
Process System Engineering Centre, University Technology Malaysia, UTM Skudai, Johor, Malysia
Z. Abdul Manan
Process System Engineering Centre, University Technology Malaysia, UTM Skudai, Johor, Malysia