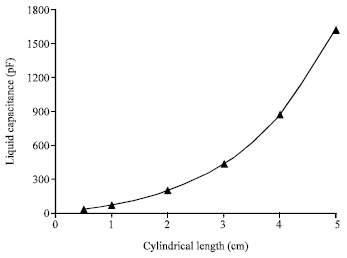
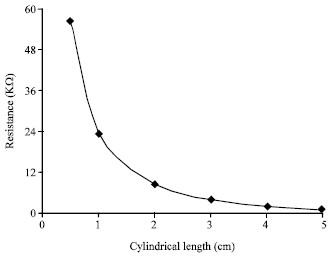
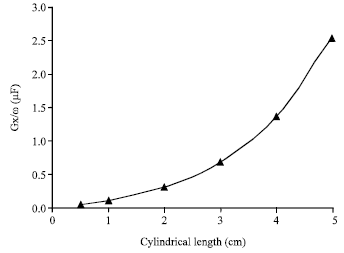
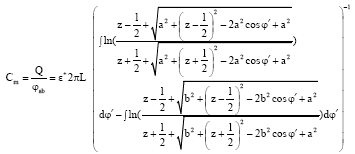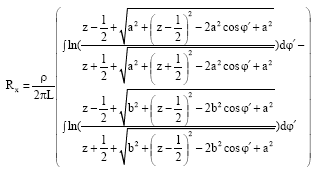Research Article
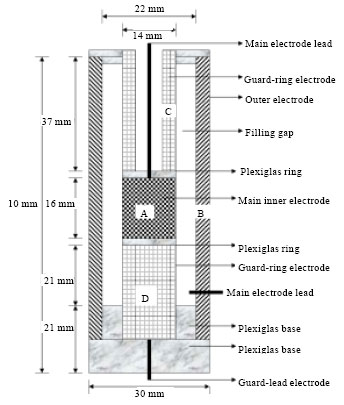
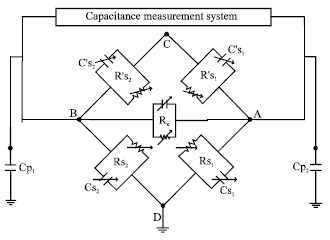
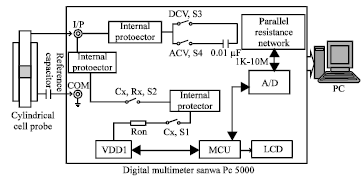
Investigation of Conductivity Effects on Capacitance Measurements of Water Liquids Using a Cylindrical Capacitive Sensor
Plasma Physics Research Center, Science and Research Branch, Islamic Azad University, P.O. Box 14665-678, Tehran, Iran
H. Golnabi
Institute of Water and Energy, Sharif University of Technology, P.O. Box 11155-8639, Tehran, Iran