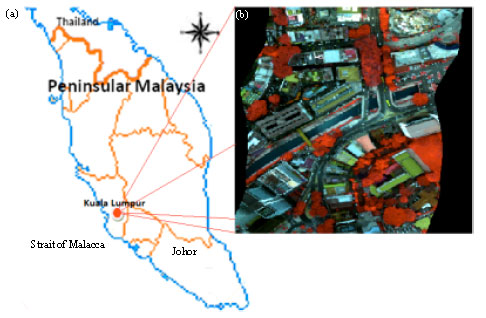
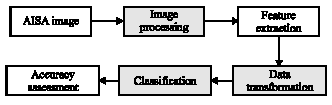
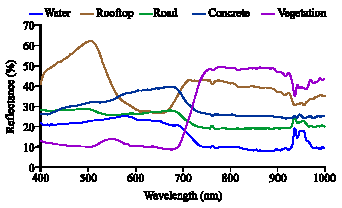
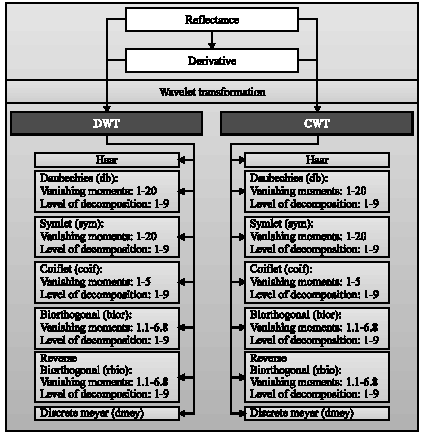
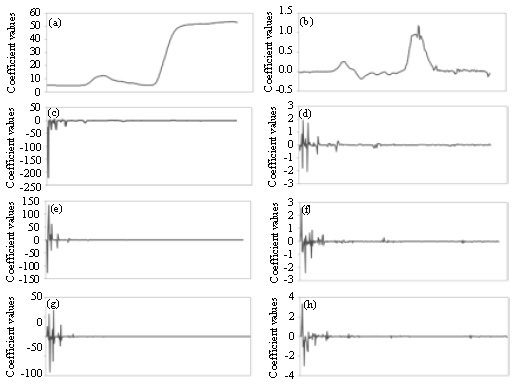
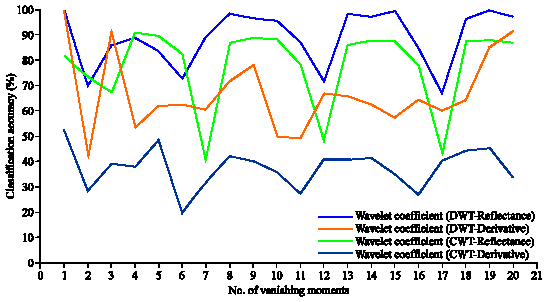
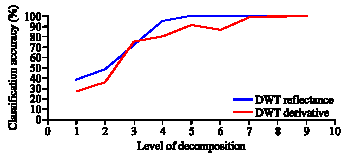
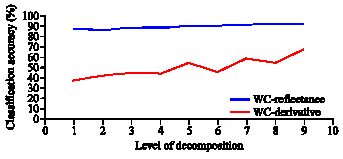
Research Article
Effects of Hyperspectral Data Transformations on Urban Inter-class Separations using a Support Vector Machine
Institute of Advanced Technology, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
H.Z.M. Shafri
Department of Civil Engineering, Faculty of Engineering, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Raja M. Kamil Raja Ahmad
Department of Electrical and Electronic Engineering, Faculty of Engineering, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia