Research Article
Wavelet-based Pre-filtering for Low Cost Inertial Sensors
Computer Systems Research Group, Department of Computer and Communication Systems, Universiti Putra Malaysia, 43400 UPM-Serdang, Malaysia
K. Samsudin
Computer Systems Research Group, Department of Computer and Communication Systems, Universiti Putra Malaysia, 43400 UPM-Serdang, Malaysia
A.R. Ramli
Intelligent Systems and Robotics Laboratory, Institute of Advanced Technology, Universiti Putra Malaysia, 43400, UPM-Serdang, Malaysia
R.S. Azmir
Wireless and Photonic Networks (WiPNET) Research Center of Excellence,Universiti Putra Malaysia, 43400, UPM-Serdang, Malaysia










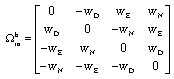
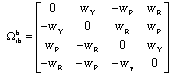
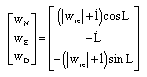
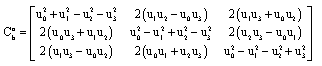
Xavier Piao Reply
This article seems very intuitive to understand the main points.
Thank you for your effort.
But I am poor in this area...
so actually to implement this Wavelet Denoising in real time system like MEMS IMU processing, I should know its real-time scheme and should know how long delay from it according to its decomposition level.
Output delay seems somewhat long if this denoising is proceeded I think.
In a word, could you kindly let me know what is the real-time implementing algorithm step by step?
Or any detailed literature for it in IMU sensor output processing.
I am so eager to hear from you.
Thank you in advance.
I hope your reply soon.
With Best Regards,
Xavier Piao, China.