Research Article
Unsteady MHD Flow and Heat Transfer over a Stretching Plate
School of Mathematical Sciences, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor, Malaysia
The steady laminar boundary layer flow over a continuously stretching plate was first studied by Crane (1970), who obtained an exact solution to the Navier-Stokes equations. This problem was then extended by Afzal and Varshney (1980) to a general power law of stretching velocity uw~xm, where, x is the distance from the issuing slit and m is a constant. The value m = 0 corresponds to a moving surface with constant velocity studied by Sakiadis (1961), while m = 1 corresponds to the problem posed by Crane (1970). The development of the boundary layer due to a stretching permeable sheet was studied by Gupta and Gupta (1977), who reported an exact solution for the flow field and a solution in incomplete gamma functions for the thermal field. Ali (1995) studied the general case when the sheet is stretched with stretching velocity of the form xm.
The boundary layer flow past a stretching plane surface in the presence of a uniform magnetic field, which has practical relevance in polymer processing, was studied by Pavlov (1974). Andersson (1995) then demonstrated that the similarity solution derived by Pavlov (1974) is not only a solution to the boundary layer equations, but also represents an exact solution to the complete Navier-Stokes equations. Liu (2005) extended Andersson's result by finding the temperature distribution for non-isothermal stretching sheet, both in the prescribed surface temperature and prescribed surface heat flux conditions, in which the surface thermal conditions are linearly proportional to the distance from the origin.
The heat transfer aspect for the problem posed by Crane (1970) was studied by Grubka and Bobba (1985), who reported the solution for the energy equation in terms of Kummer's functions. Several closed-form analytical solutions for specific conditions were also reported. Chen and Char (1988) investigated the effects of suction and injection on the heat transfer characteristics of a continuous, linearly stretching sheet for both the power law surface temperature and the power law surface heat flux variations. Char (1994) then studied the case when the sheet immersed in a quiescent electrically conducting fluid in the presence of a transverse magnetic field. The effect of thermal radiation on the heat transfer over a nonlinearly stretching sheet immersed in an otherwise quiescent fluid has been studied by Bataller (2008).
The unsteady boundary layer flow over a stretching sheet has been studied by Devi et al. (1991), Elbashbeshy and Bazid (2004) and quite recently by Tsai et al. (2008). The objective of the present study is to find the similarity solution for MHD flow over a linearly stretching sheet with prescribed surface temperature. The governing partial differential equations with three independent variables are transformed to ordinary differential equations using similarity transformation, before being solved numerically by the Keller-box method. The results obtained are then compared with those of Grubka and Bobba (1985) and Liu (2005) as well as the series solution for the steady-state flow case to support their validity.
PROBLEM FORMULATION
Consider an unsteady, two-dimensional laminar boundary layer flow over a continuously stretching plate immersed in an incompressible electrically conducting fluid. At time t = 0, the plate is impulsively stretched with the velocity Uw (x, t) along the x-axis, keeping the origin fixed in the fluid of ambient temperature T∞. The stationary Cartesian coordinate system has its origin located at the leading edge of the plate with the positive x-axis extending along the plate, while the y-axis is measured normal to the surface of the plate. A transverse magnetic field of strength B is assumed to be applied in the positive y-direction, normal to the surface. The induced magnetic field is assumed to be small compared to the applied magnetic field and is neglected. The simplified two-dimensional equations governing the flow are:
| (1) |
| (2) |
| (3) |
where, u and v are the velocity components along the x and y axes, respectively, T is the fluid temperature in the boundary layer, t is time and v, ρ and α are the kinematic viscosity, fluid density and thermal diffusivity, respectively. We shall assume that the boundary conditions of Eq. 1-3 are:
| (4) |
We assume that the stretching velocity Uw (x,t) and the surface temperature Tw (x, t) are of the form:
| (5) |
where a, b and c are constants with a>0, b≥0 and c≥0 (with ct<1) and both a and b have dimension time-1. It should be noticed that at t = 0 (initial motion), Eq. 1-3 describes the steady flow over a stretching surface. This particular form of Uw (x, t) and Tw (x, t) has been chosen in order to be able to devise a new similarity transformation, which transforms the governing partial differential Eq. 1-3 into a set of ordinary differential equations, thereby facilitating the exploration of the effects of the controlling parameters (Andersson et al., 2000). Further, to obtain similarity solutions of Eq. 1-4, we assume that the unsteady magnetic field B is of the form ![]() , where B0 is a constant.
, where B0 is a constant.
The continuity Eq. 1 is satisfied by introducing a stream function ψ such that:
| (6) |
The momentum and energy equations can be transformed into the corresponding ordinary differential equations by the following transformation:
 | (7) |
The transformed ordinary differential equations are:
| (8) |
| (9) |
where, primes denote differentiation with respect to η, M = σB20/(ρa) is the magnetic parameter, A = c/a is a parameter that measures the unsteadiness and Pr is the Prandtl number. The boundary conditions (4) now become:
f(0) = 0, f'(0) = 1, θ (0) = 1 |
| (10) |
We note that when A = 0 (steady-state flow), the problem under consideration reduces to those considered by Liu (2005) for prescribed surface temperature case, while when A = 0 and M = 0 (without magnetic field) the present problem reduces to those of Grubka and Bobba (1985), for which an exact analytical solution was reported.
The physical quantities of interest are the skin friction coefficient Cf and the local Nusselt number Nux, which are defined as:
| (11) |
where, the surface shear stress τw and the surface heat flux qw are given by:
| (12) |
with μ and k being the dynamic viscosity and thermal conductivity, respectively. Using the non-dimensional variables Eq. 7, we obtain:
| (13) |
where, Rex = Uwx/v is the local Reynolds number.
When A = 0, the problem under consideration reduces to the steady-state flow, where the exact solution for the flow field is given by:
| (14) |
and the solution for the thermal field in terms of Kummer's functions is:
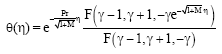 | (15) |
where, γ = Pr/(1+M) and F (a, b, z) denotes the confluent hypergeometric function (Abramowitz and Stegun, 1965), with:
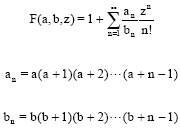 |
By using Eq. 14 and 15, the skin friction coefficient f" (0) and the local Nusselt number -θ' (0) can be shown to be given by:
| (16) |
| (17) |
Moreover, when Pr = 1 and M = 0, the solution θ (η) given by Eq. 15 can be expressed as θ(η) = f' (η) = e-η, which implies:
| (18) |
The nonlinear ordinary differential Eq. 8 and 9 subject to the boundary conditions Eq. 10 were solved numerically by means of an implicit finite-difference scheme known as the Keller-box method as described in the books by Keller (1971) and Cebeci and Bradshaw (1988), for several values of A, M and Pr. This method has been successfully used by the present author to solve various boundary-value problems (Ishak et al., 2010a-d).
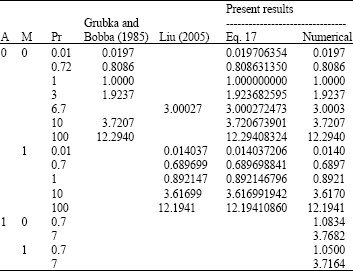
The step size Δη in η and the position of the edge of the boundary layer η∞ have to be adjusted for different values of parameters to maintain the necessary accuracy. In this study, the values of Δη between 0.001 and 0.1 were used, depends on the values of the parameters used, in order that the numerical values obtained are independent of Δη chosen, at least to four decimal places. However, a uniform grid Δη = 0.01 was found to be satisfactory for a convergence critirion of 10-5 which gives accuracy to four decimal places, in nearly all cases. On the other hand, the boundary layer thickness η∞ between 6 and 50 was chosen where the infinity boundary conditions are achieved. To assess the accuracy of the present method, comparison with previously reported data available in the literature, as well as the series solution for the steady-state case, is made for several values of A, M and Pr, as given in Table 1, which shows an excellent agreement.
Figure 1 and 2 present the velocity profiles for different values of A and M, respectively, when the other parameter is fixed. From both figures, it is seen that the velocity gradient at the surface increases (in magnitude) with both A and M. Thus, the magnitude of the skin friction coefficient |f"(0)| increases as A or M increases. This observation is in agreement with the series solution for the steady-state case given by Eq. 16. Figure 1 and 2 as well as Eq. 16 show that the velocity gradient at the surface f"(0) is negative for all values of parameters considered. Physically, negative values of f" (0) means the solid surface exerts a drag force on the fluid. This is not surprising since the development of the velocity boundary layer is caused solely on the stretching plate.
| Table 1: | Values of -θ'(0) for various values of A, M and Pr |
 | |
 | |
| Fig. 1: | Velocity profiles f' (η) for different values of A when M = 1 |
 | |
| Fig. 2: | Velocity profiles f' (η) for different values of M when A = 1 |
Further, the velocity is found to decrease as the distance from the surface increases and reaches the boundary condition at infinity asymptotically. We note that, the Prandtl number Pr gives no influence to the development of the velocity boundary layer, which is clear from Eq. 8.
In many practical applications, the characteristics involved, such as the heat transfer rate at the surface are vital since they influence the quality of the final products. The temperature profiles presented in Fig. 3 show that the temperature gradient at the surface increases (in magnitude) as A increases, which implies an increase of the heat transfer rate at the surface -θ' (0). The same phenomenon is observed for the variation of θ(η) with Pr as can be seen from Fig. 4, i.e., the heat transfer rate at the surface increases with increasing Pr. This can be explained as a higher Prandtl number fluid has a relatively low thermal conductivity, which reduces conduction and thereby the thermal boundary layer thickness and as a consequence increases the heat transfer rate at the surface (Chen and Char, 1988). Conversely, the absolute value of the temperature gradient at the surface decreases with an increase in M, as shown in Fig. 5. Thus, the heat transfer rate at the surface decreases with increasing M. Though the magnetic parameter does not directly enter into the energy equation, it actually affects the velocity distribution and therefore increases the temperature profile indirectly (Liu, 2005).
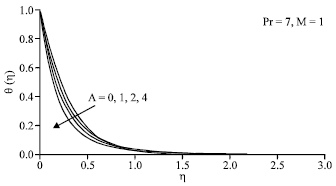 | |
| Fig. 3: | Temperature profiles θ(η) for different values of A when Pr = 7 and M = 1 |
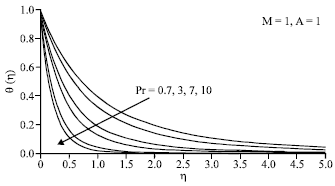 | |
| Fig. 4: | Temperature profiles θ(η) for different values of Pr when M = 1 and A = 1 |
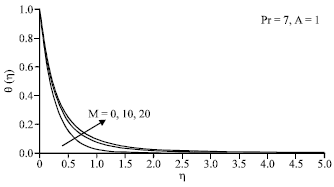 | |
| Fig. 5: | Temperature profiles θ(η) for different values of M when Pr = 7 and A = 1 |
It can be observed from Fig. 3-5 that θ(η) decreases to zero so as to meet the far field boundary condition θ(∞) = 0 asymptotically for all values of parameters considered.
Finally, we note that in the absent of the magnetic field, the velocity profile is identical to the temperature profile, i.e., f' (η) = θ(η), for Prandtl number unity.
The problem of unsteady MHD boundary layer flow and heat transfer due to a stretching plate immersed in an electrically conducting fluid was investigated numerically. The effects of the governing parameters, namely the unsteadiness parameter A, magnetic parameter M and Prandtl number Pr on the fluid flow and heat transfer characteristics were thoroughly examined. The numerical results obtained are comparable very well with previously reported cases, as well as the series solution for the steady-state case. It was found that the heat transfer rate at the surface -θ'(0) increases with A and Pr, but decreases with M.
This study was supported by a research grant (Project Code: 06-01-02-SF0610) from the Ministry of Science, Technology and Innovation (MOSTI), Malaysia.