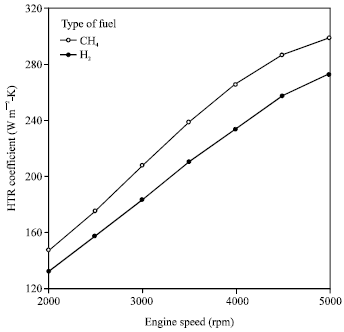
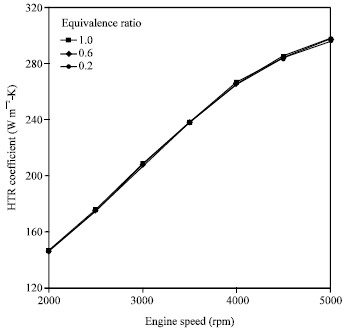
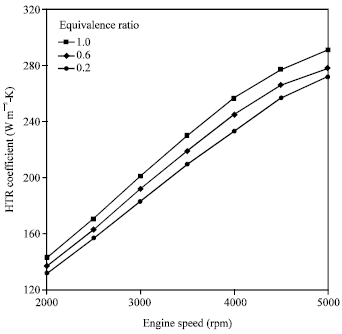
Research Article
Heat Transfer Characteristics of Intake Port for Spark Ignition Engine:A Comparative Study
Department of Mechanical Engineering, University Malaysia Pahang, 26600 Pekan, Kuantan, Pahang, Malaysia Automotive Excellence Center, University Malaysia Pahang, 26600 Pekan, Kuantan, Pahang, Malaysia
K.I. Hamada
Department of Mechanical Engineering, University Malaysia Pahang, 26600 Pekan, Kuantan, Pahang, Malaysia
M.M. Noor
Department of Mechanical Engineering, University Malaysia Pahang, 26600 Pekan, Kuantan, Pahang, Malaysia
K. Kadirgama
Department of Mechanical Engineering, University Malaysia Pahang, 26600 Pekan, Kuantan, Pahang, Malaysia
M.A. Maleque
Department of Manufacturing and Material, Engineering Faculty of Engineering, International Islamic University Malaysia, Gombak, Selangor, Malaysia
R.A. Bakar
Department of Mechanical Engineering, University Malaysia Pahang, 26600 Pekan, Kuantan, Pahang, Malaysia