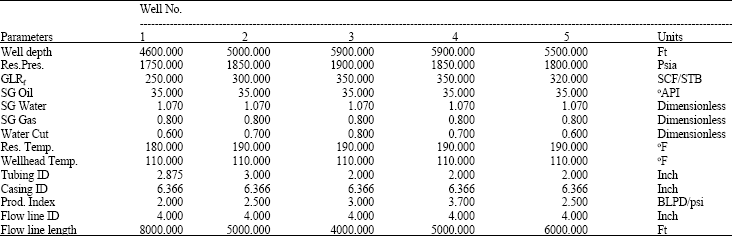
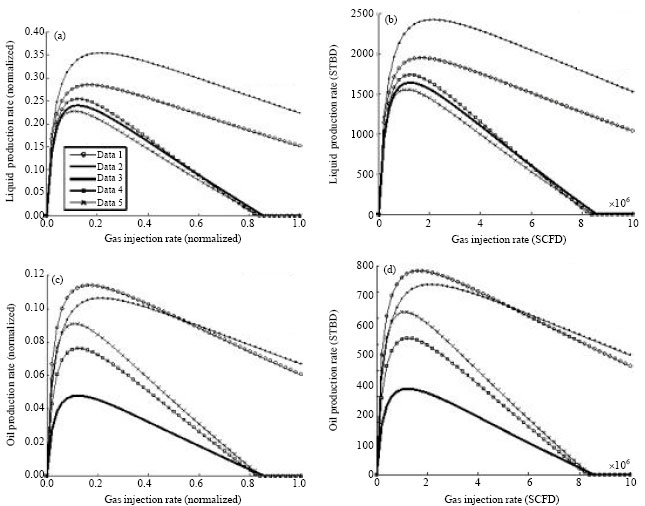
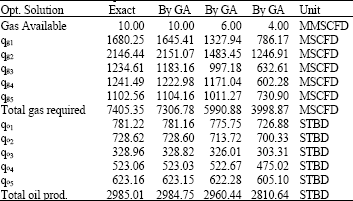
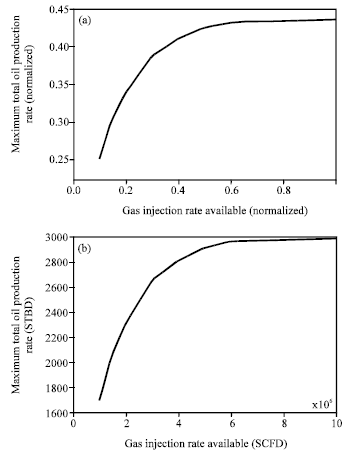
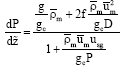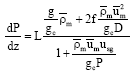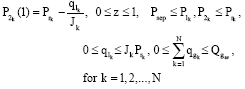Research Article
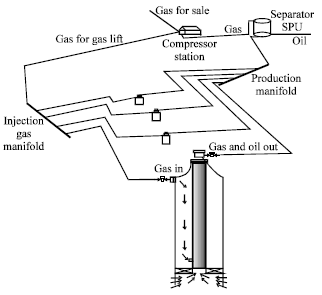
Oil Production Optimization in a Cluster of Gas Lift Wells System
Program Studi Ilmu Komputasi, Insitut Teknologi Telkom, Jl. Telekomunikasi No. 1, Bandung 40257, Indonesia
Pudjo Sukarno
Drilling and Production Engineering and Oil and Gas Management Research Group, Institut Teknologi Bandung, Jl. Ganeca 10 Bandung 40132, Indonesia
Edy Soewono
Financial and Industrial Mathematics Research Group, Institut Teknologi Bandung, Jl. Ganeca 10 Bandung 40132, Indonesia
Kuntjoro Adji Sidarto
Financial and Industrial Mathematics Research Group, Institut Teknologi Bandung, Jl. Ganeca 10 Bandung 40132, Indonesia
Agus Yodi Gunawan
Financial and Industrial Mathematics Research Group, Institut Teknologi Bandung, Jl. Ganeca 10 Bandung 40132, Indonesia