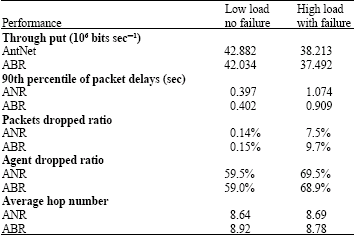
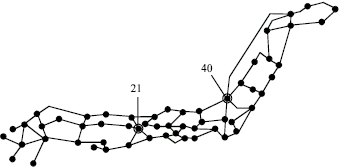
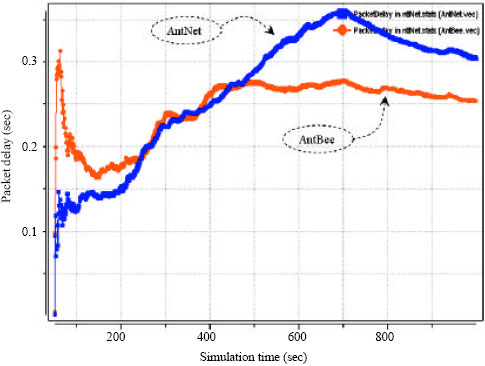
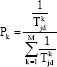Research Article
The Ant-Bee Routing Algorithm: A New Agent Based Nature-Inspired Routing Algorithm
Department of Electrical and Computer Engineering, Shahid Beheshti University, Tehran, Iran
H. Shah-Hosseini
Department of Electrical and Computer Engineering, Shahid Beheshti University, Tehran, Iran
H. Torkaman
Department of Electrical and Computer Engineering, Shahid Beheshti University, Tehran, Iran