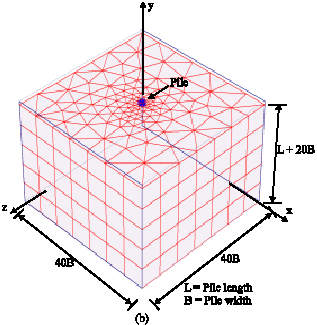
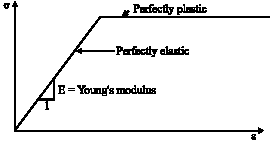
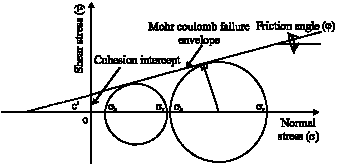
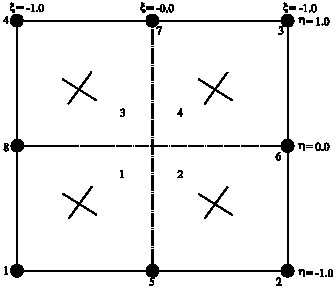
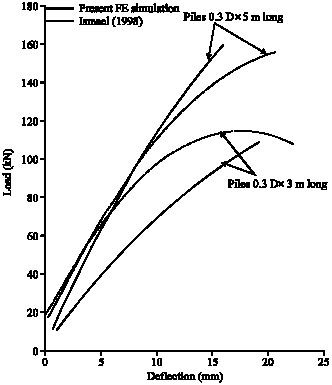
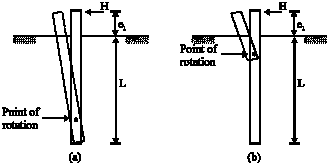
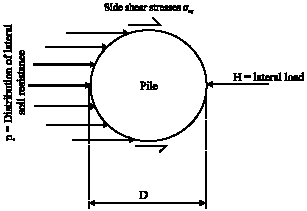
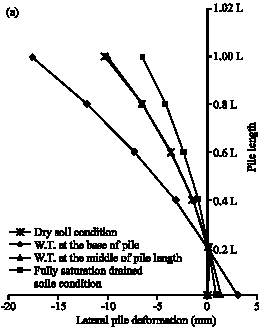
Research Article
The Performance of Laterally Loaded Single Pile Embedded in Cohesionless Soil with Different Water Level Elevation
Department of Civil and Structural Engineering, Universiti Kebangsaan Malaysia, Selangor, Malaysia
Jasim M. Abbas
Department of Civil and Structural Engineering, Universiti Kebangsaan Malaysia, Selangor, Malaysia
Qassun S. Mohammed Shafiqu
Department of Civil Engineering, Nahrain University, Iraq
Zamri H. Chik
Department of Civil and Structural Engineering, Universiti Kebangsaan Malaysia, Selangor, Malaysia