Research Article
Algorithm Based Fault Tolerant and Check Pointing for High Performance Computing Systems
University of Isfahan, Isfahan, Iran
A. Vafaei
University of Isfahan, Isfahan, Iran
A.H. Monadjemi
University of Isfahan, Isfahan, Iran
Algorithm based fault tolerance (Huang and Abraham, 1984) is a class of approaches which tolerant byzantine failures, in which failed processors continues to work but produce incorrect calculations. In this approach, applications are modified to operate on encoded data to determine the correctness of some mathematical calculations. This class of approaches can mainly be applied to applications performing linear algebra computations and usually achieves a very low overhead. One of the most important characteristics of this research is that it assumes a fail-continue model in which failed processors continues to work but produce incorrect calculations. A major concern in fault tolerant systems design is to provide the desired fault tolerance within the available cost, power consumption, performance constraints, etc. It has been shown that in certain matrix applications, low overhead fault tolerance can be achieved using ABFT (Huang and Abraham, 1984; Acree et al., 1993). Errors occur with different rates depending on the environments where computing systems are operated. For example, satellites experience error rates based on their altitude and location. This variation makes different fault tolerance schemes more appropriate in different environments. ABFT technique is distinguished by three characteristics:
| • | Encoding the input data stream |
| • | Redesign of the algorithm to operate on the coded data |
| • | Distribution of the additional computational steps among the various computational units in order to exploit maximum parallelism |
The input data are encoded in the form of error detecting or correcting codes. The modified algorithm operates on the encoded data and produces encoded data output, from.
Which useful information can be recovered very easily? Obviously, the modified algorithm will take more time to operate on the encoded data when compared to the original algorithm; this time overhead must not be excessive. The task distribution among the processing elements should be clone in such a way that any malfunction in a processing element will affect only a small portion of the data, which can be detected and corrected using the properties of the encoding. Signal processing has been the major application area of ABFT until now, even though the technique is applicable in other types of computations as well. Since the major computational requirements for many important real-time signals processing tasks can be formulated using a common set of matrix computations, it is important to have fault tolerance techniques for various matrix operations (Nair and Abraham, 1990). Coding techniques based on ABFT have already been proposed for various computations such as matrix operations (Huang and Abraham, 1984; Baylis, 1998), FFT (Jou and Abraham, 1988), QR factorization and singular value decomposition (Chen and Abraham, 1986). Real number codes such as the Checksum (Huang and Abraham, 1984) and Weighted Checksum codes (Jou and Abraham, 1986) have been proposed for fault-tolerant matrix operations such as matrix transposition, addition, multiplication and matrix-vector multiplication. Application of these techniques in processor arrays and multiprocessor systems has been investigated by various researchers (Reddy and Banerjee, 1990; Aykanat and Ozguner, 1987; Banerjee et al., 1990). In order to illustrate the application of ABFT techniques, we discuss fault tolerant matrix operations in detail. We present some previous results in the area and then present some new results related to encoding schemes for fault-tolerant matrix operations (Hamidi and Mohammadi, 2005).
Figure 1 (Nia and Mohammadi, 2007) shows the basic architecture of an ABFT system. Existing techniques use various coding schemes to provide information redundancy needed for error detection and correction. As a result this encoding/decoding must be considered as the overhead introduced by ABFT. The coding algorithm is closely related to the running process and is often defined by real number codes generally of the block types (Jou and Abraham, 1986). Systematic codes are of most interest because the fault detection scheme can be superimposed on the original process box with the least changes in the algorithm and architecture. In most previous ABFT applications, the process to be protected is often a linear system. In this study we assume a more common case consisting linear or nonlinear systems but still constrain ourselves to static systems.
Single-failure recovery model: This model, consisting of N application processors and m spare processors, can handle m single failures during the lifetime of the application. The program executes on N processors, there is a single check pointing processor. Figure 2 and 3 show how to construct checkpoints and how to recover in the presence of a single failure. As shown, a spare processor becomes the new check pointing processor after recovery, if one is available. The model therefore tolerates m single failures (Kim, 1996; Plank et al., 1995; Chen and Dongarra, 2008).
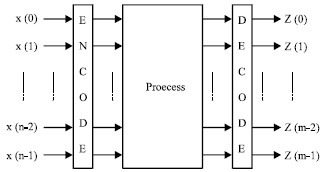 | |
| Fig. 1: | General architecture of ABFT |
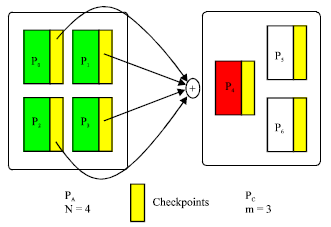 | |
| Fig. 2: | Single-failure recovery model: before a failure |
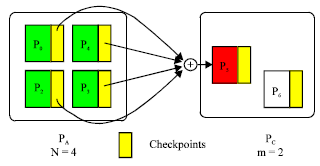 | |
| Fig. 3: | A multiple-failure recovery model |
Multiple-failure recovery model: A generalization of the single-failure recovery model, the multiple-failure recovery model consists of n + m processors that can tolerate m failures at once. Instead of having one dedicated processor for check pointing, the entire set of application processors is divided into m groups and one check pointing processor is dedicated to each group. When one failure occurs in a group, the check pointing processor in the group will replace the failed one and the application will roll back and resume at the last checkpoint. Figure 4 shows the application processors logically configured into a two dimensional mesh, with a check pointing processor dedicated to each row of processors (Kim, 1996; Plank et al., 1995; Chen and Dongarra, 2008).
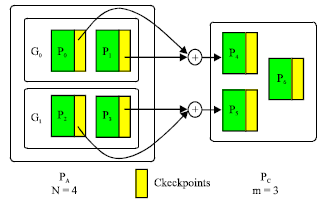 | |
| Fig. 4: | A multiple-failure recovery model |
This model enables the algorithm to tolerate a certain set of multiple failures simultaneously, one failure for each. This is often called the one dimensional parity scheme (Hamidi and Mohammadi, 2006). Several schemes have been developed to configure extra check pointing processors to tolerate multiple processor failures. For example, the paper (Hamidi and Vafaei, 2009) presents two dimensional parity or multidimensional parity, in which the coding information is distributed in two dimensional or multidimensional fashion, respectively. Burkhard and Menon (1993) introduces EVENODD parity, with which two extra processors may be used to tolerate any two failures in the system. More complicated coding schemes have been suggested to tolerate m failures with m check pointing processors for arbitrary m (Chen and Dongarra, 2005a, b; Wang et al., 2007).
Basic concepts: In matrix operations, we assume that an m x n input matrix A is partitioned into square blocks, each of an equal block size b. With such matrix partitioning, a sequential block algorithm of matrix operations is performed in steps, one for each column of blocks, which is called a column block. For a parallel implementation, the partitioned matrix A is distributed among the NP processors logically reconfigured as a P*Q mesh using two dimensional block cyclic data distribution, where NP = PxQ. Therefore, each processor holds m/P row blocks and n/Q column blocks of block size b, where it is assumed that P and Q divide m and n, respectively. Figure 5 shows the block cyclic data distribution of a matrix with 6*6 blocks over a 2*2 mesh of four processors. Various block algorithms exist for matrix factorizations. In the following subsections, we start with a brief description of block algorithms of matrix factorizations. The remaining matrix operations are discussed when their fault tolerant algorithms are described (Kim, 1996; Plank et al., 1995).
 | |
| Fig. 5: | Data distribution of a matrix with 6*6 blocks over a 2*2 mesh of processors |
Weighted checksum encoding: Many ABFT techniques utilize a general weighted checksum encoding for matrices (Hamidi and Vafaei, 2009; Chiang et al., 2009). In this representation, an n*n matrix is modified by adding to it additional rows and columns to store the row/column sums and weighted row/column sums. If eT = [11111…1] and etw [20 21 22…2n], the (n*n)*(n*n) full weighted checksum matrix for the n*n matrix A, in block form, becomes:
 | (1) |
as described by Hamidi and Vafaei (2008). A column or row weighted checksum matrix would include only the column checksums or only the row checksums, respectively. The un weighted sums, of the form Ae or AeT, are denoted as WCS1; the exponentially weighted sums, of the form Aew or eTw A, are denoted as WCS2. A single fault, affecting only one matrix element, can be detected and located and the resulting error corrected after a matrix operation using this scheme. For the location and correction of a single error, Jou and Abraham (1986) introduce the variables S1and S such that:
| (2) |
| (3) |
where, a = (a1, a2,…, an) represents either a row or a column vector. S1 represents the error in the un-weighted checksum; S2 denotes the error in the weighted checksum. If the two errors S1 and S2 are non-zero, (s2/s1) = 2j-1 implies that aj is the incorrect element. The faulty value may then be corrected by making aj = â-s1. Using this scheme, Jou and Abraham (1986) provide fault-tolerant algorithms for a number of signal processing and matrix operations (Rexford and Jha, 1992).
 | (4) |
Thus the element αj is incorrect. The faulty value may then be corrected by making:
| (5) |
We consider now the multiplication of matrices A and B. The weighted checksum matrices are:
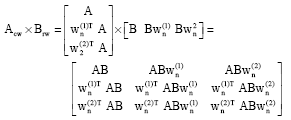 |
or
 |
or
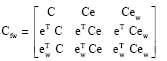 | (6) |
Then
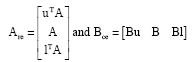 | (7) |
Where:
| (8) |
and
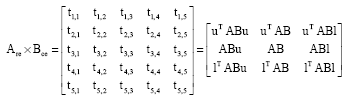 | (9) |
where, calculated C is:
 | (10) |
A procedure used to detect, locate and correct a single erroneous element is the following:
Error detection: Step 1: Compute the following sums Table 1.
Error location: An error will be located according to the follow Table 2.
Error correction: The erroneous element can be corrected by adding the difference between the computed sum of the erroneous block sum information elements and the equivalent element of matrix D to the erroneous element.
| (11) |
| Table 1: | For error detection computes the following sums |
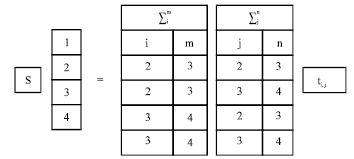 | |
| Table 2: | An error will be located according to the follow |
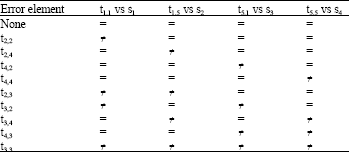 | |
LU factorization: In LU factorization, an m x n real matrix A is factored into a lower triangular matrix L and a upper triangular matrix U, i.e., PA = LU, where P is a permutation matrix At each iteration, one column block is factored and a permutation matrix P is generated, if necessary, The LU factorization is performed in place and P is stored as a one dimensional array of the pivoting indices. Three variants exist for implementing LU factorization on sequential machines. These three block algorithms of LU factorization can be constructed as follows. Suppose that we have factored A as A = LU. We write the factors in block form as follows:
 | (12) |
With these relationships, we can develop three variants by manipulating the order in which computations are formed and maintaining the final result of computations in place. These variants are called ijk variants (Kim, 1996; Plank et al., 1995; Dongarra et al., 1991; Postalcioglu and Erkan, 2009) or, more specifically, right-looking, top-looking and left looking, respectively. They differ in which regions of data are accessed and computed during each reduction step. Figure 6 shows the different data access patterns among the three variants.
Cholesky factorization: Cholesky factorization factors an n*n real, symmetric, positive definite matrix A into a lower triangular matrix L and its transpose LT, i.e., A = LLT or UTU where, U is upper triangular). Because of the symmetric, positive definite property of the matrix A, Cholesky factorization is also performed in place on either an upper or lower triangular matrix and involves no pivoting. Three different variants of the Cholesky factorization can be developed Kim (1996) and Plank et al. (1995).
QR factorization: Given an m *n real matrix A, QR factorization factors A such that:
| (13) |
where, Q is an m*m orthogonal matrix and R an n*n upper triangular matrix, Q is computed by applying a sequence of Householder transformations to the current column block of the form, Hi = 1-τiviviT where, i =1… b. In one block QR algorithm-Q can be applied or manipulated through the identity Q = H1 H2…Hb = 1-VTVT where V is a lower triangular matrix of Householder vectors Vi and T isan upper triangular matrix constructed from the triangular factors Vi and τi of the Householder transformations.
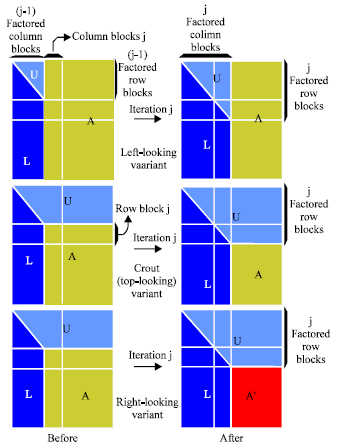 | |
| Fig. 6: | Three variants of LU factorizations (Kim, 1996) |
When the factorization is complete, V is stored in the lower triangular part of the original matrix A, R is stored in the upper triangular part of A and the ti are stored in the diagonal entries of A. The complete details of this algorithm are described in by Hamidi and Vafaei (2008), Ekici et al. (2009) and Naghipour et al. (2008). Both left-looking and right looking variants can be constructed (Kim, 1996; Plank et al., 1995).
Analysis of check pointing and recovery: The basic check pointing operation works on a panel of blocks, where each block consists of X floating-point numbers and the processors are logically configured in a P*Q mesh (Fig. 7). The processors take the checkpoint with a combine operation of XOR or addition. This works in a spanning tree fashion in three parts. The checkpoint is first taken row wise, then taken column wise and then sent to PC. The first part therefore takes [log P] steps and the second part takes [log Q] steps. Each step consists of sending and then performing either XOR or addition on X floating point numbers. The third part consists of sending the X numbers to PC. We define the following terms:
 | |
| Fig. 7: | Check pointing the matrix of Fig. 5 (Kim, 1996) |
| γ | : | The time for performing a floating point addition or XOR operation |
| α | : | The start up time for sending a message |
| β | : | The time to transfer one floating point number |
The first part takes [log P] (α+X(β+γ)), the second part takes [log Q] (α+X(β+γ)) and the third takes (α+Xβ).
IMPLEMENTATIONS
The fault tolerant matrix operations described in the preceding chapter were implemented in the PVM programming environment (Geist et al., 1994; Wang et al., 2009). The failure free versions of the matrix operations were implemented as part of APACK (Choi et al., 1996a). The ScaLAPACK library includes core matrix operations developed by using two subroutine libraries: The PB_BLAS and the BLACS. The PB_BLAS (Parallel Block-Based Linear Algebra Subprograms) (Choi et al., 1996b) are an extended subset of the Level and 2 BLAS 3 (Dongarra et al., 1990) for distributed-memory computers. The BLACS (Basic Linear Algebra Communication Subprograms) (Dongarra and Whaley, 1995) perform common matri oriented communication tasks. Both of these subroutine packages are also implemented in the PVM programming environment. The fault-tolerant implementations were designed to provide the user with the same efficiency, high performance and portability as the ScaLAPACK routines. We first developed the overall structure of the fault tolerant versions of the underlying libraries by embedding failure detection and identification using the fault-tolerant features of PVM (Geist et al., 1994). All aspects of fault tolerance were kept internal to the applications and as transparent to the programmer as possible. The structure of these implementations is depicted in Fig. 8.
 | |
| Fig. 8: | Structure of the fault-tolerant implementations (Kim, 1996) |
For all of the implementations, the following set of tests was performed and timed:
| • | Failure free algorithm without check pointing |
| • | Fault tolerant implementation with single check pointing |
| • | Single check pointing implementation with one random failure |
| • | Fault tolerant implementation with multiple check pointing |
| • | Multiple check pointing implementations with multiple failures |
Note that the failures were forced to occur at the last iteration before the first checkpoint. The performance results of the implementations are evaluated in terms of the following parameters:
| • | Total elapsed wall-clock times of the algorithms in seconds (TA, T) |
| • | Check pointing and recovery overheads in seconds (TC, TR) |
| • | Check pointing interval in iterations (K, NC = n/Kb) |
| • | Average check pointing interval in sec ((T-Tinit)/NC) |
| • | Average checks pointing overhead in sec (ΔTC) |
| • | Total size of checkpoints in bytes (M) |
| • | Extra memory usage in bytes (Mc) |
| • | Check pointing rate in bytes per second (R) |
Performance evaluation: The check pointing performed in these implementations consists of data communication and either XOR or addition of floating point numbers. We define the check pointing rate R as the amount of data check pointed in bytes per second. This metric has been used to evaluate the performance of various check pointing schemes (Elnozahy et al., 1992).
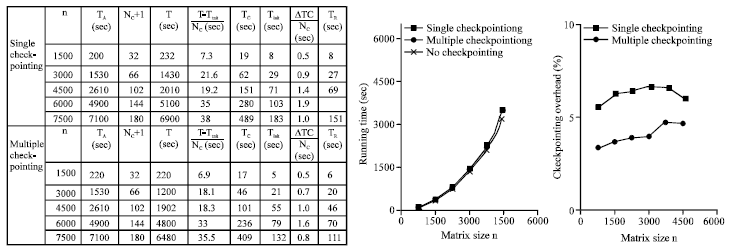 | |
| Fig. 9: | Left-looking LU, timing results |
 | |
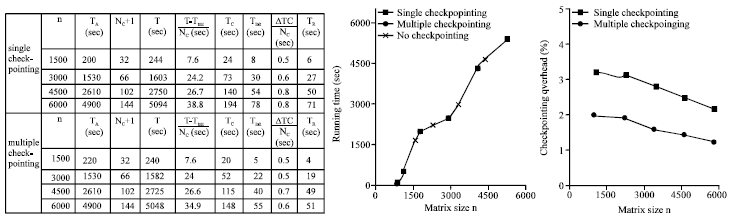
| Fig. 10: | Left-looking Cholesky, timing results |
In our case, the check pointing rate is determined experimentally based on our analytic models of the fault-tolerant implementations. This check pointing rate is used to compare the performance of the different fault tolerance techniques, Fig. 12 and 13 plot the check pointing rate for each implementation.
Parity-based technique: For the parity-based matrix operations, the total percentage overhead of check pointing decreases as the problem size n increases.
The total overhead of recovery is dominated by the time for taking the bitwise exclusive-or of each processor’s entire data. The time it takes to recover does not depend upon the location of the failure.
The multiple check pointing implementations show performance improvement. LU factorizations benefit relatively more from the multiple checks pointing because of pivoting.
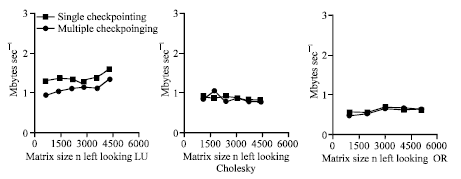
Figure 10 shows the check pointing rate experimentally determined for each implementation this presents the overall performance of the parity-based technique for matrix operations. Since the measured peak bandwidth of the network is 64 M bits sec-1, we expect that the check pointing rate should be somewhat lower than 8 M bytes sec-1 considering synchronization, copying, performing XOR and message latency and network contention. As shown in Fig. 12 and 13 the check pointing rate determined experimentally is between 2 and 4 M bytes sec-1 for all the matrix operations. The right-looking variant performs the best among the failure-free variants of each factorization because it benefits from less communication and more parallelism than the others. However, for the LU and Cholesky factorizations, left-looking variants with check pointing perform better than the right-looking variant with check pointing. For the QR factorization, no top-looking variant exists and the left-looking variant performs much slower than the right-looking variant. The total check pointing overhead of the left-looking variant is too high compared with the right-looking variant without check pointing (Fig. 9-11).
 | |
| Fig. 11: | Left-looking QR, timing results |
 | |
| Fig. 12: | Experimental check pointing rate |
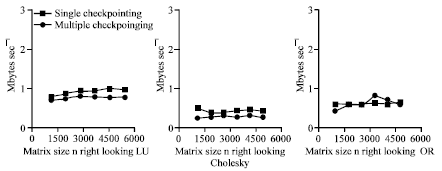 | |
| Fig. 13: | Experimental check pointing rate |
The fault-tolerant matrix operations can be characterized as follows: Very low overhead while check pointing at a relatively fine-grain interval, Robust and easy to incorporate this technique into numerical algorithms. Check pointing and recovery does not cause numerical problems such as overflow and underflow. Block size has little impact on check pointing and recovery overhead. Usefulness is limited to those matrix operations in which a moderate amount of data is modified between two checkpoints. The numerical results of the multiple check pointing technique confirm that the technique is more efficient and reliable by not only distributing the process of check pointing and rollback recovery over groups of processors but also by tolerating multiple failures in one of each group of processors. This technique has been shown to improve both the reliability of the computation and the performance of the check pointing and recovery. In particular, for the checksum and reverse computation based implementations, multiple check pointing could reduce the check pointing and recovery overhead without using more memory. In addition, the probability of overflow, underflow and cancellation error can be reduced. Finally, it is easier to develop fault tolerant implementations when multiple check pointing processors are used for check pointing and recovery. This study presents a paradigm for executing certain scientific computations on a changing distributed computing platform. The paradigm allows a distributed computation to run on a platform where individual processors may leave due to failures, unavailability, or heavy load and where processors may enter during the computation. Algorithm based fault tolerance techniques efficiently exploit the semantics of the application at low cost in programmer effort. The programming effort to render applications fault-tolerant is justifiable when the fault tolerant implementations are provided as numerical libraries. The paradigm provides an interesting way to allow reliability in computations performed on networks of computers. The paradigm supports a heterogeneous network of workstations. The paradigm an be adapted to the algorithms based on any data distribution, rather than being specific to the block cyclic distribution employed in the current implementations. We emphasize that our scheme can be used to detect data corruption in a system where such detection is otherwise absent. In coding theory terms, our mechanism can provide detection in an error-prone environment or correction in an erasure environment. Fault tolerance is normally not provided in such parallel and distributed computing platforms.