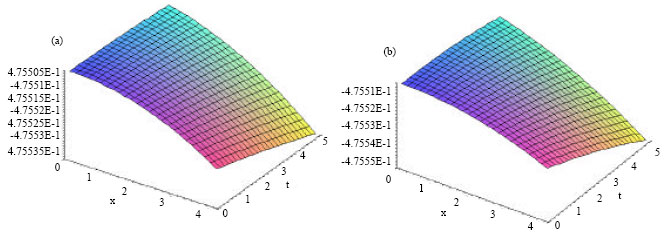
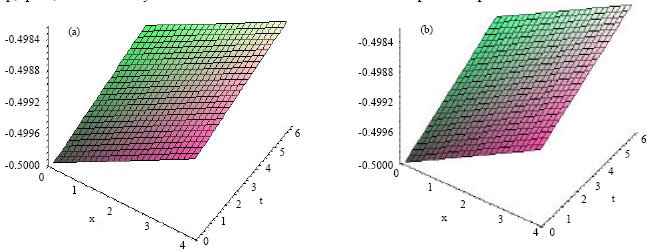
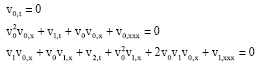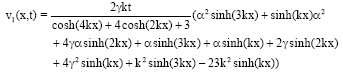Research Article
Application of Homotopy Perturbation Method to Solve Combined Korteweg de Vries-Modified Korteweg de Vries Equation
School of Mechanic, Islamic Azad University, Jouybar Branch, Jouybar, Iran
D.D. Ganji
Department of Mechanical Engineering, Babol Nushirvani University of Technology, P.O. Box 484, Babol, Iran