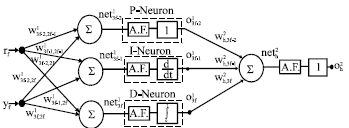
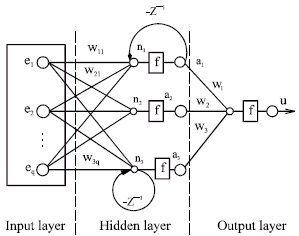
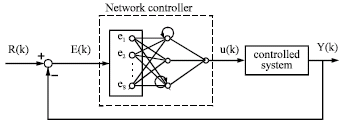
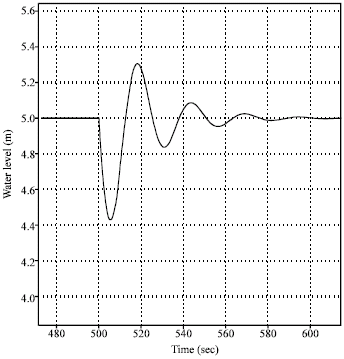
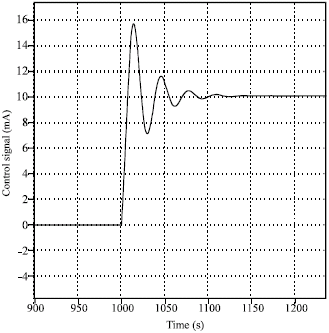
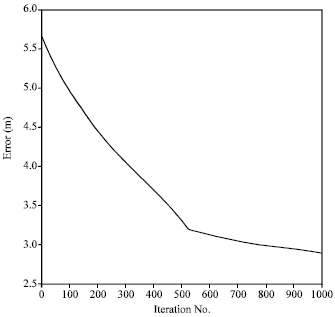
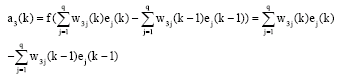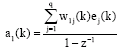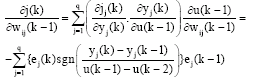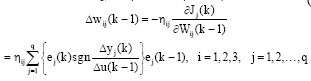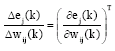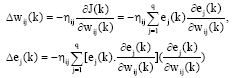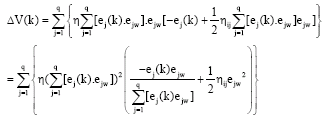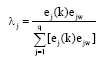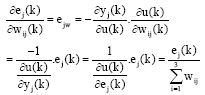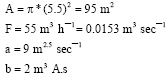Research Article
Adaptive Neuro-PID Controller Design with Application to Nonlinear Water Level in NEKA Power Plant
Faculty of Electrical Engineering, Power and Water University of Technology, Tehran, Iran
A. Mehrafrooz
Faculty of Electrical Engineering, Power and Water University of Technology, Tehran, Iran
J. Jouzdani
Department of Electrical Engineering, Amirkabir University of Technology, Tehran, Iran
R. Barzamini
Department of Electrical Engineering, Amirkabir University of Technology, Tehran, Iran