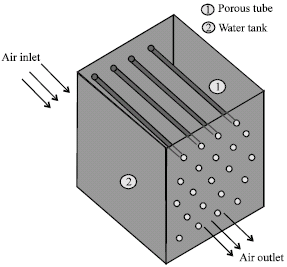
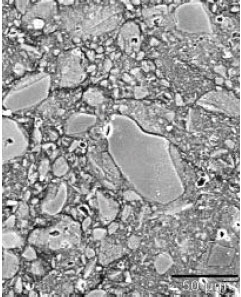
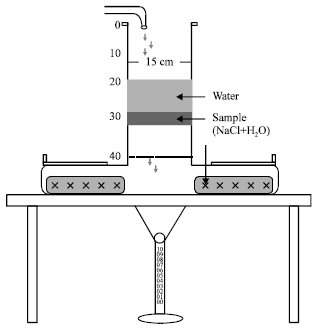
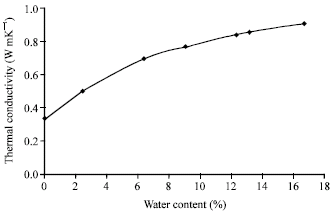
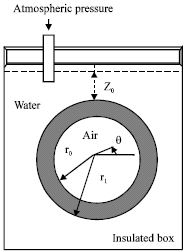
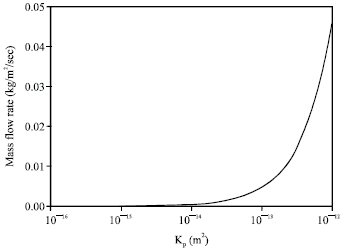
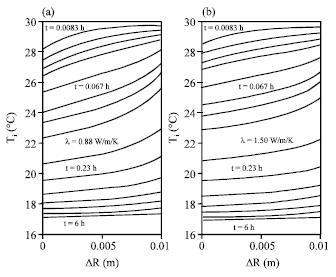
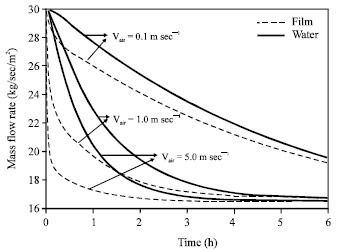
Research Article
Experimental Determination of Some Micro-Structural and Hydrous Properties of a Terra Cotta and Modelisation of Hygrothermal Transfers
Laboratoire d’Energies Thermiques Renouvelables, Département de Physique, UFR Sciences Exactes et Appliquées, Université de Ouagadougou, BP 7021, Burkina Faso
J. Bathiebo
Laboratoire d’Energies Thermiques Renouvelables, Département de Physique, UFR Sciences Exactes et Appliquées, Université de Ouagadougou, BP 7021, Burkina Faso
L. Zerbo
Laboratoire de Physico-Chimie et de Technologie des Matériaux, Département de Chimie-UFR Sciences Exactes et Appliquées, Université de Ouagadougou, BP 7021, Burkina Faso
J. Soro
Groupe d’étude des Matériaux Hétérogènes, Ecole Nationale Supérieure de Céramique Industrielle, 47 Avenue A. Thomas 87065, Limoges Cedex, France
K. Traore
Laboratoire de Physico-Chimie et de Technologie des Matériaux, Département de Chimie-UFR Sciences Exactes et Appliquées, Université de Ouagadougou, BP 7021, Burkina Faso
P. Blanchart
Groupe d’étude des Matériaux Hétérogènes, Ecole Nationale Supérieure de Céramique Industrielle, 47 Avenue A. Thomas 87065, Limoges Cedex, France
F. Kieno
Laboratoire d’Energies Thermiques Renouvelables, Département de Physique, UFR Sciences Exactes et Appliquées, Université de Ouagadougou, BP 7021, Burkina Faso