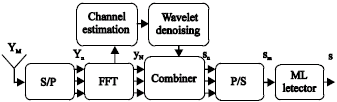
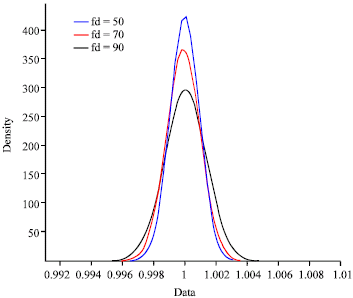
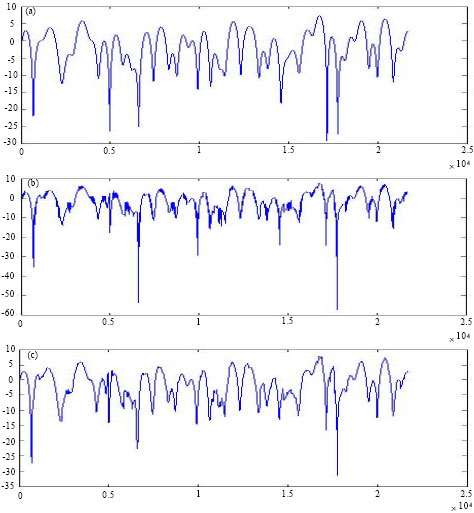
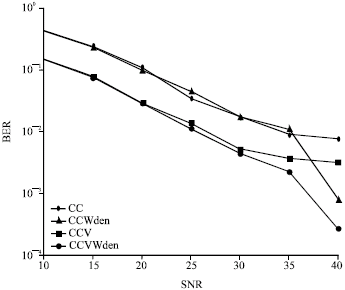
Research Article
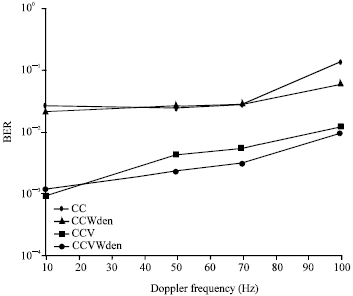
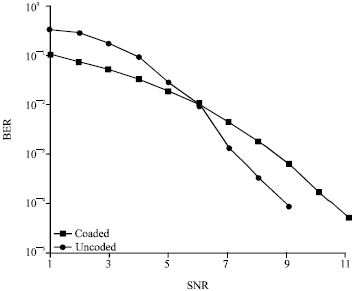
TCM and Wavelet De-Noising Over an Improved Algorithm for Channel Estimations of OFDM System Based Pilot Signal
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, National University of Malaysia, 43600 UKM Bangi Selangor Darul Ehsan, Malaysia
M. Ismail
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, National University of Malaysia, 43600 UKM Bangi Selangor Darul Ehsan, Malaysia
M.A. M. Ali
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, National University of Malaysia, 43600 UKM Bangi Selangor Darul Ehsan, Malaysia
K. Jumari
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, National University of Malaysia, 43600 UKM Bangi Selangor Darul Ehsan, Malaysia