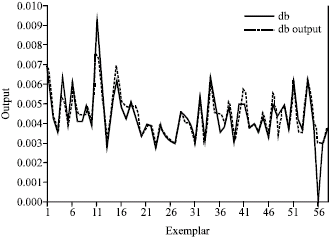
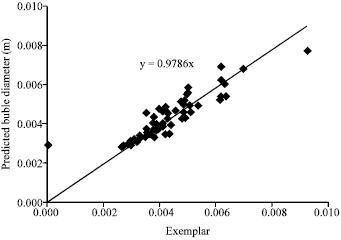
Research Article
Prediction of Bubble Size in Bubble Columns using Artificial Neural Network
Department of Chemical Engineering, University of Malaya 50603, Kuala Lumpur, Malaysia
Mohamed A. Hussain
Department of Chemical Engineering, University of Malaya 50603, Kuala Lumpur, Malaysia