Research Article
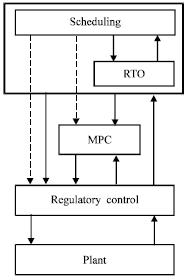
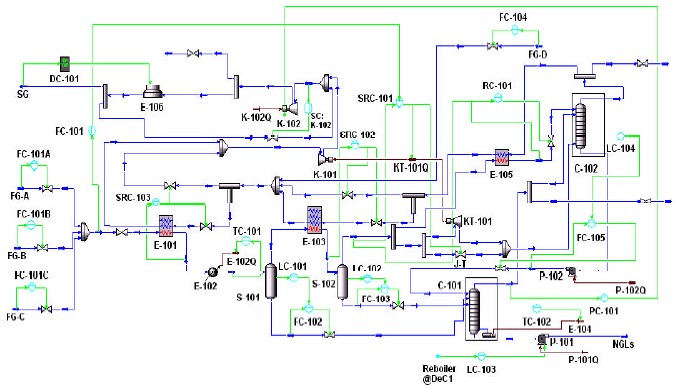
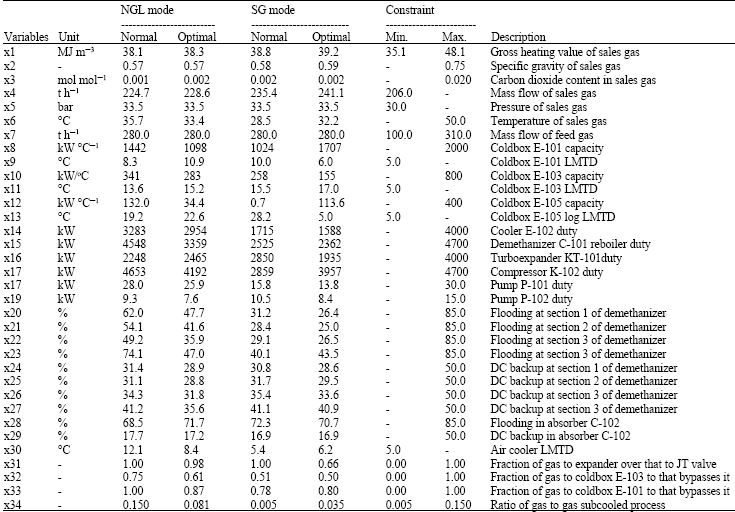
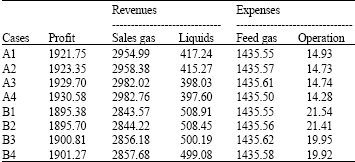
Integrated Scheduling and RTO of RGP with MPC and PI Controllers
Department of Chemical Engineering, Universiti Teknologi PETRONAS, 31750 Tronoh, Perak, Malaysia
M. Ramasamy
Department of Chemical Engineering, Universiti Teknologi PETRONAS, 31750 Tronoh, Perak, Malaysia