Research Article
Redundancy for Reliability Growth of Electronic Systems under Various Operating Conditions
Department of Electrical Engineering, Ferdowsi University of Mashhad, Postal Code 9177948974, Mashhad, Iran
Analysis of system reliability in both Europe and the United States is as old as the 1940s when the main thrust was behind aerospace applications with severe operating conditions and life-threatening missions. Such studies were later applied to other areas. However, they still remain the most important subject in sensitive applications like military, aerospace and life-critical medical electronics. An early study considering reliability issues in navigation systems dates back to 1966 where a reliability analysis was performed on the Navigation and Flight Instruments subsystem of the Boeing B-2707. Lyngaas and Watson (1966) reported a study that was aimed at determining whether the reliability goals could be met or not and identifying the hardware or human factors which are expected to pose reliability problems. Rogge (1974) reported a study of the reliability of Inertial Navigation System (INS) reliability. He considered the effect of flying hours programs on MTBF and showed that the Time Between Overhaul (TBO) is the best measurement of INS reliability for the TRC.
Agrawala et al. (1992) reported the development of a domain-specific software architecture for intelligent (adaptive) guidance, navigation and control for aerospace applications. In their study the need to adapt to a variety of specialized target hardware systems, requirements for high reliability and system certification and increasing demands for functional integration and high performance computing were presented. The approach used by Agrawala et al. (1992) exhibits three major themes: an extensive reliance on formal models, a provision of multiple views corresponding to multiple areas of skills and requirements and an open toolset and layered architecture. The importance of reliability was stressed in this study by considering the importance of fault tolerance, security, testing and plant model verification. However, their software approach to the problem is not useful in the system under study in this paper, since the present system is already operational and no changes in its software or structure are possible, except for the use of hardware redundancy.
Boyd and Bavuso (1992) reported the use of reliability modelling and simulation to evaluate the reliability of a hypercube multiprocessor architecture for guidance, navigation and control systems for long duration manned spacecraft. They used simulation to evaluate homogeneous Markovian, non-homogeneous Markovian and non-Markovian models of the hypercube by focusing on the effect of assuming Weibull decreasing component failure rates compared to the usual assumption of constant component failure rates. They also studied the effect of the use of cold spares on system reliability under the assumption of both constant and Weibull decreasing failure rates.
Goodchild (1993) reported the operation of a system that will estimate either the local-relative or absolute-global position of Unmanned Underwater Vehicles (UUVs). The Seastar system which was presented by Goodchild (1993) allowed for both autonomous and remote controlled navigation of UUVs. However, its configuration is such that it lacks any redundancy and is thereby not very reliable. There is a single navigation computer in their system. Its output is used for three UUV functions, namely the Autonomous UUV Control, including autopilot, attitude and heading and area navigation; guidance and navigation data for acoustic link transmissions to the sea surface segment for UUV monitoring and remote control and guidance and navigation monitoring data for sea surface operations during deployment and recovery. They only rely on duplicate communication links between the UUV and command and control vessel using a direct acoustic link as well as acoustic/radio links by the buoys.
One possible approach to reliability improvement is integration of parts into more modern components with a higher reliability. Integration of discrete parts using modern VLSI gates such as FPAAs and FPGAs are presented as a means of improving system reliability by Peiravi (2008). The improvement in reliability can also be achieved by other means such as accelerated life testing, derating of parts as shown by Peiravi (2009) and use of redundancy in design. The present study stresses the effect of the use of redundancy in design in order to improve reliability where the use of other viable alternative approaches is not feasible.
THE CASE STUDY SYSTEM
The case study system in this research that is subject to reliability growth program is mainly responsible for navigation and guidance and monitors all sensitive devices by receiving their status and issues proper warning signals to the operator in case any problems arise. The initial system was composed of a single navigation and guidance computer as shown in Fig. 1.
In order to improve the reliability different measures could be adopted. Reliability could be improved by using more reliable parts on the system. However, since this product is already a highly reliable product, it used high quality parts to begin with and it was not possible to improve its reliability by using more reliable parts. Another option is to integrate several parts into a single more reliable part. This was also out of the question for the present system since the system already used modern VLSI components which are highly integrated. The next viable option to improve the reliability of the system was derating of parts. However, this was only feasible in a small portion of the system, more specifically in its panel, the power supply and the interface board. Still this could not bring about the required reliability improvement that was desired.
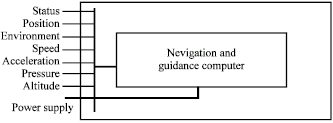 | |
| Fig. 1: | The initial navigation and guidance system without redundancy |
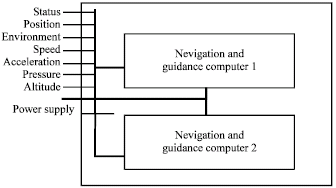 | |
| Fig. 2: | Navigation and guidance system with redundancy |
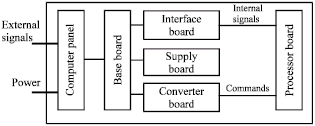 | |
| Fig. 3: | The interconnections between the various subsystems of the navigation and guidance computer |
Therefore, the last alternative for reliability improvement being the use of redundancy was chosen in this study. The use of two navigation and guidance computers instead of one was proposed in order to improve the reliability. Therefore, the navigation and guidance computer in the system was doubled up as shown in Fig. 2. The type of redundancy used is active in that once one computer fails, the other may be substituted automatically to take over its functions.
The various subsystems of the navigation and guidance computer are briefly shown in Fig. 3. It consists of a digital processor board, an interface board, a converter board, a power supply board, a base board and a panel which is used to provide the interface between the system and the operator. The electrical schematics and the wiring tables are not needed here, even though they were studied in detail in order to see how each subsystem's functioning affected the overall system's function to determine the reliability block diagram of each board, each subsystem and the overall system.
MEASURES OF RELIABILITY
The lifetime of a component is a stochastic variable which is often used in reliability studies. Certain operations on the probability distribution function of this stochastic variable may be used as measures of reliability. The mean time to failure or MTTF is the average time that a given part operates before it fails. It may be computed from the probability distribution function of time to failure ![]() as follows:
as follows:
The mean time to repair or MTTR is the average time that a given part is in the failed state before it is repaired and brought back into service. It may be computed from the probability distribution function of time to failure ![]() as follows:
as follows:
The mean time between failures or MTBF is the average cycle time for a part to operate before it fails and be repaired after it fails and be brought back into service. It may be computed from the MTTF and the MTTR as follows:
The failure rate λ(t) and the repair rate μ(t) are each defined as follows:
And the reliability of the system may be found from the failure rate function as follows:
The probability of failure is the same as unreliability and may be computed from the following:
System availability gives the probability that the system would perform its expected function at an unknown time t in the future for a repairable system and it may be computed as follows:.
whereas, unavailability is given as:
THE FAILURE RATE AND THE EFFECT OF OPERATING CONDITIONS
The failure rate of electronic parts depends on many factors and is usually shown in the following general form:
where, πE denotes an application environment coefficient, f denotes a function of, πT denotes a temperature coefficient, πQ denotes a quality factor coefficient and πS denotes a stress coefficient.
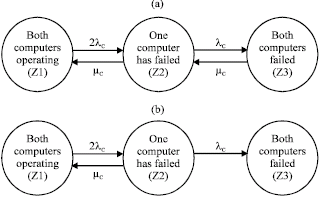
For various parts, there are various coefficients to be used and there may be more factors which influence the failure rate of a device. Reliability data can be obtained from various organizations which maintain and provide such data as shown in Table 1.
The application environment coefficient denoted by πE refers to the expected operating conditions of the system under study. There are certain generic classifications of expected operating conditions which are normally used to calculate an estimate of the failure rate. These operating conditions are classified in various ways by different organizations. Table 2 shows the classifications used by the Department of Defense as per MIL-HDBK-217F (1995).
| Table 1: | The various sources for failure rate data |
 | |
| Table 2: | The generic operating conditions per mil-handbk-217F |
 | |
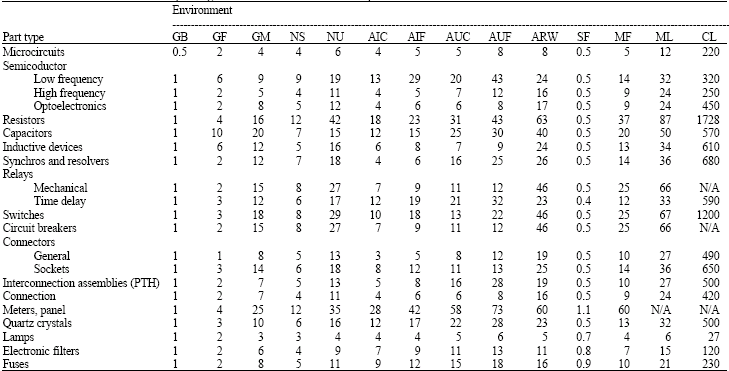
| Table 3: | The various coefficients of operating conditions for various electronic parts |
 | |
| N/A: Not available | |
The various coefficients of operating conditions for various electronic parts are shown in Table 3.
MODELING AND SIMULATION
One may use various reported techniques in any reliability study. In this study, the reliability has been estimated using RBD and state space approach, repairability has been studied using Monte Carlo simulations and availability has been studied using the state space approach. The failure rate of the system was estimated using the RBD approach and then the reliability was computed. The reliability block diagram for each navigation and guidance computer is shown in Fig. 4. In a given series system, the failure rate of the system may be computed from the failure rate of the individual parts making up that system as follows:
The failure rate may be computed by using a spreadsheet for the navigation and guidance system with redundancy. Then the reliability may be computed as follows:
Reliability prediction in the initial stages of product life is an important issue. One has to rely on some existing data bases such as EPRD, NPRD, MIL-217F, etc. This issue is addressed in Vintr (2007), where internationally accepted and the most common tools in the field of reliability prediction such as EPRD-97, NPRD-95, SPIDR™ and the reliability prediction methods MIL-HDBK-217F, PRISM©, FIDES, 217Plus™, RDF 2000, Telcordia SR-332, GJB/z 299B, NSWC-98/LE1 are discussed.
| Fig. 4: | The reliability block diagram for each navigation and guidance computer |
In this study, the failure rate data were obtained from the most common of these data sources such as MIL-HDBK-217F (1995) or EPRD.
The equivalent part for nr redundant parts in parallel is computed as follows:
THE STATE SPACE MODEL OF THE SYSTEM
The inclusion of a redundant computer in the navigation and guidance system improves the reliability of the system. The state space model of the navigation and guidance system with redundancy is shown in Fig. 5a assuming the possibility of repair after both computers fail and is shown in Fig. 5b assuming that it is not possible to repair the second one after both fail (as it may be the case in some scenarios).
The state space model can be solved using the following equations:
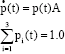 |
where, p(t) is a row vector indicating the state probabilities, p0,p1,p2. The matrix A is formed using the transition rates shown in Fig. 5a and b.
This system is solved and the resulting probabilities may be used to find the reliability measures. In either case, the probability of system success is the same as the probability of the first state, or p0. The mean time to failure is as follows:
The system availability is as follows:
And the system reliability is as follows:
 | |
| Fig. 5: | The state space diagram of the proposed system assuming (a) repair after both fail and (b) no repair after both fail |
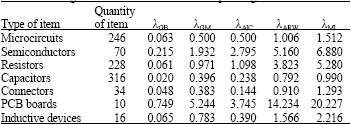
| Table 4: | A summary of various electronic parts, their quantity and their average failure rates under different operating conditions |
 | |
| Table 5: | The overall estimated failure rates for the various subsystems of the navigation and guidance computer in failures per million hours without using redundancy |
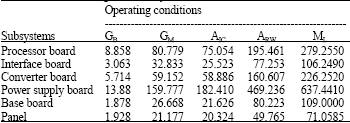 | |
The system reliability is computed for five different operating conditions of ground benign GB,ground mobile GM, airborne, inhabited, cargo, AIC, airborne, rotary, winged, ARW and missile launch, ML..The overall estimated failure rates for the various subsystems of the navigation and guidance computer in failures per million hours are shown in Table 5. As shown in Table 5, it can be seen that the failure rates are much higher in more severe operating conditions. Table 6 shows the failure rate and MTTC for one navigation and guidance computer while Table 7 shows the reliability measures for the navigation and guidance system considering various operating environments without using redundancy.
The mean time to repair MTTR for the navigation and guidance computer is:
| Table 6: | The failure rate and MTTC for one navigation and guidance computer |
 | |
| Table 7: | Reliability measures for the navigation and guidance system considering various operating environments without using redundancy |
 | |
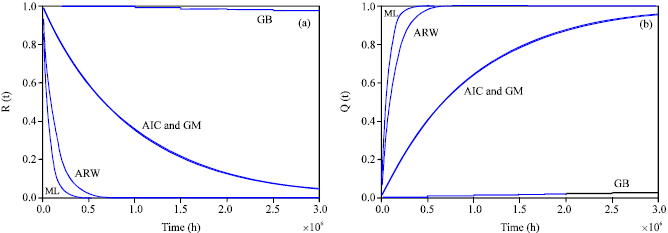 | |
| Fig. 6: | (a) Reliability R(t) and (b) Failure probability of the navigation and guidance control system for various operating conditions without using redundancy |
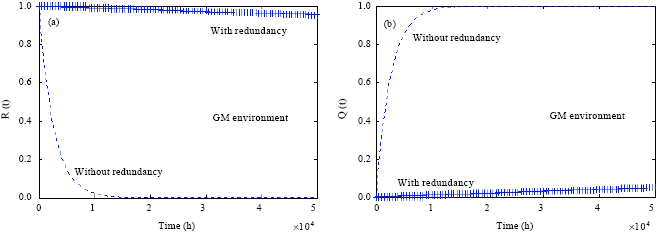 | |
| Fig. 7: | The effect of using a redundant computer in the navigation and guidance control system, (a) shows the reliability while and (b) shows the failure probability |
The reliability of the navigation and guidance computer may be found using the mean time to failure shown in the Table 4-7. For example, the reliability under AIC operating conditions is as follows:
The reliability and the failure probability of the original navigation and guidance system without redundancy and the proposed redundant system are shown in Fig. 6a and b for 3000000 h of operation.
The effect of using a redundant computer in the navigation and guidance system on the reliability improvement and reduction of the failure probability in ground mobile conditions can be easily shown from Fig. 7. As one may show from Fig. 7a, the reliability of this system after 5000 h of operation is 81.5% more than the case where there is no redundant computer used in the system. Figure 7b shows that the probability of failure is also improved drastically using a redundant flight computer.
Expected operating conditions are very important in the analysis of the reliability of navigation and guidance systems. The availability of such systems depends upon their MTTF and MTTR. Therefore, a modular design which helps reduce the repair time is very important in improving the reliability of the whole system. The inclusion of redundancy in design is very effective in reliability improvement, especially in sophisticated equipment where not much else can be done to improve system reliability.
I hereby acknowledge the support of the Office of International Cooperation, Office of Applied Research for the military research grant and the Office of the Vice Chancellor of Research and Technology of the Ferdowsi University of Mashhad for their support.