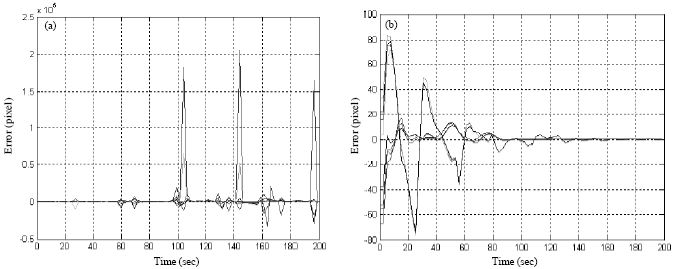
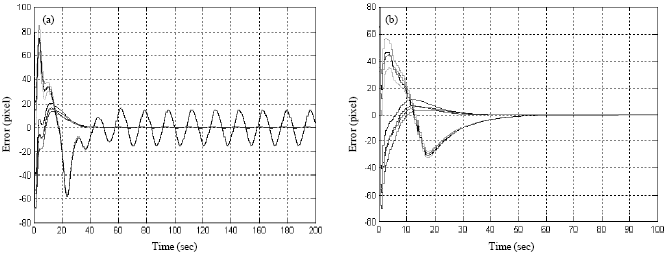
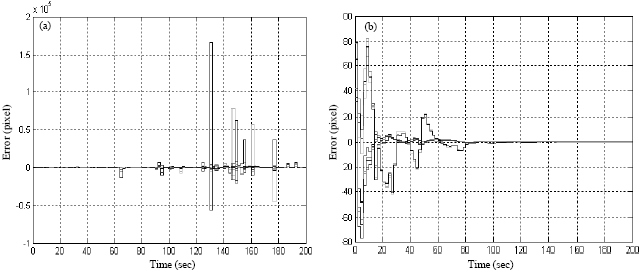
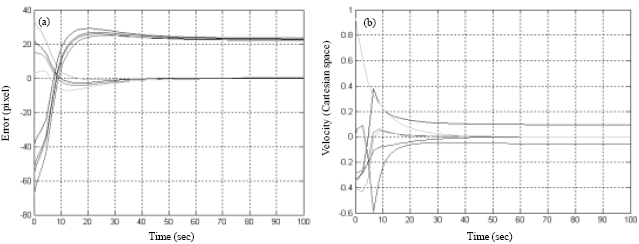
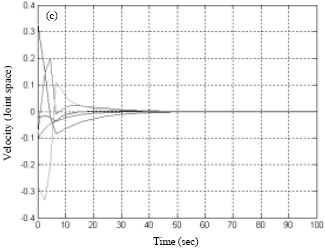
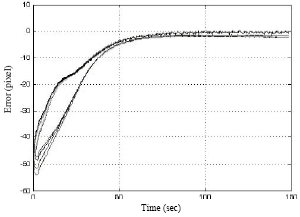
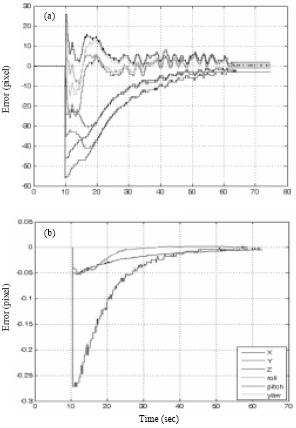
Research Article
Tele-Visual Servoing of Robotic Mamipulators; Design, Implementation and Technical Issues
Research Laboratory of Robotics, Department of Control Engineering, Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran
H. Jabbari Asl
Research Laboratory of Robotics, Department of Control Engineering, Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran