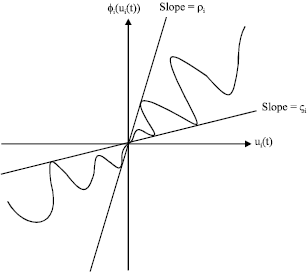
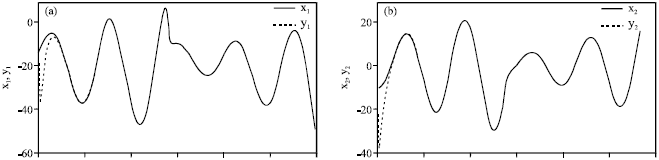
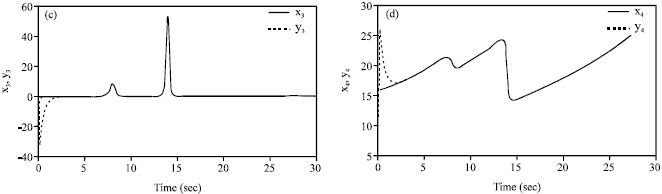
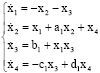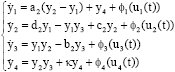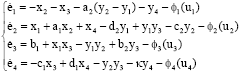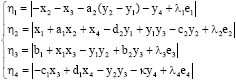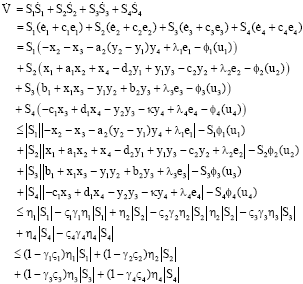Research Article
Design of Variable Structure Synchronization Controller for Two Different Hyperchaotic Systems Containing Nonlinear Inputs
Department of Electrical Engineering, Far-East University, No. 49, Jung-Hwa Road, Hsin-Shih Town Tainan 744, Taiwan, Republic of China
Cheng-Chi Wang
Department of Mechanical Engineering, Far-East University, No. 49, Jung-Hwa Road, Hsin-Shih Town Tainan 744, Taiwan, Republic of China
Neng-Sheng Pai
Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 411, Taiwan, Republic of China