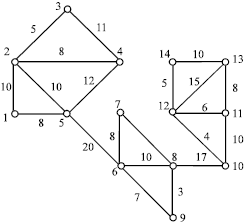
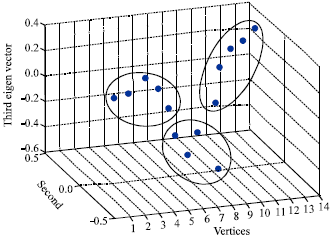
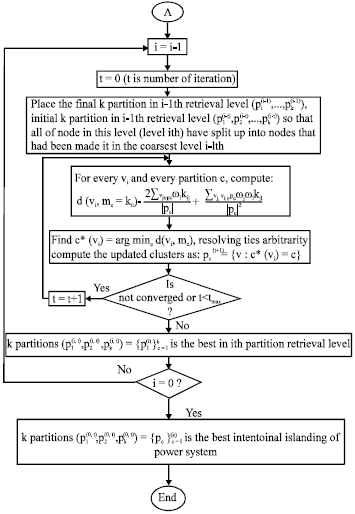
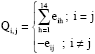Research Article
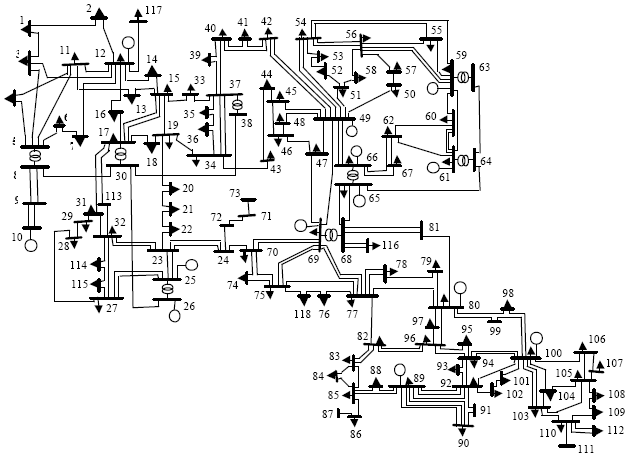
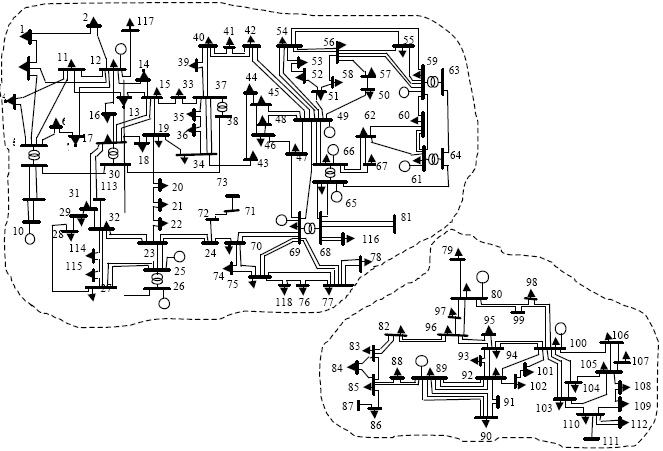
A Fast Algorithm for Intentional Islanding of Power Systems Using the Multilevel Kernel k-Means Approach
Department of Electrical Engineering, School of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran
R. Ildarabadi
Department of Electrical Engineering, School of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran