Research Article
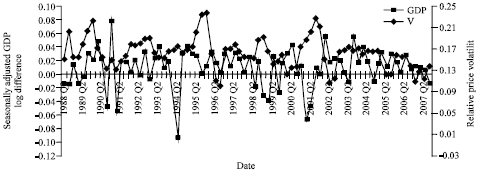
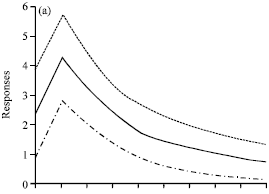
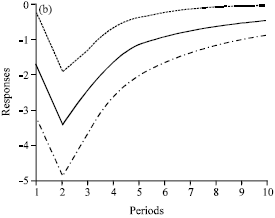
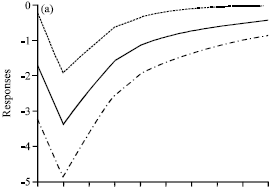
The Choice of Monetary Policy Tool(s) and Relative Price Variability: Evidence from Turkey
Department of Economics, Bilkent University, 06800 Ankara, Turkey
A. Sahin
Republic of Turkey, Ministry of Agriculture and Rural Affairs, Department of Foreign Relations and European Union, Eskisehir Yolu, 9 km Lodumlu, 06530 Ankara, Turkey
B. Saracoglu
Department of Econometrics, Gazi University, 06500 Ankara, Turkey










Alfred Book Reply
Very interesting and essential paper for the economic literature.