ABSTRACT
This study assesses the management of reactive power generation to improve the voltage stability margin using modal analysis technique. The simulation results show that after the optimal reactive power re-scheduling, the voltage stability margin of the system is improved and the active/reactive power losses are decreased. Improving the voltage stability margin of power system without adding new VAR (Volt Ampere Reactive) sources and changing the active power dispatch, is the most important advantage of proposed method.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2009.2123.2129
URL: https://scialert.net/abstract/?doi=jas.2009.2123.2129
INTRODUCTION
The problem of voltage instability is gaining more and more importance in recent years. Because of the growth of power systems and inefficient reactive power management. The voltage control service connected to reactive power supply is one of the fundamental factors to guarantee stability and security of power systems. The voltage instability is strongly associated with the lack of reactive power support in the system caused by limitations in the generation or transmission of the reactive power. Because of the continuous increase of power demands, modern power systems are operated in proximity of their maximum operation limits. Under such conditions, voltage instability of the systems likely occurs. Since, optimization technique was applied to power system analysis, Optimal Power Flows (OPF) have been widely used in planning and real-time operation of power systems for active and reactive power dispatch to minimize generation costs and system losses and to improve system VSM. Optimal reactive power dispatch (ORD) is a sub-problem of the OPF calculation. ORD determines all kinds of controllable variables, such as reactive-power outputs of generators and static VAR (Volt Ampere Reactive) compensators, tap ratios of transformers, outputs of shunt capacitors/reactors and etc., achieving an adequate VSM and minimizing transmission losses or other appropriate multi objective functions are general ORD objectives. ORD optimization should satisfy a given set of physical and operating constraints (Zhao et al., 2005; Esmin et al., 2005; Yan et al., 2006; Venkatesh et al., 2000; Hooshmand, 2008).
Voltage stability problem has received much attention in recent years and has been a target concern during planning and operation of heavily loaded and complex power systems. One of the most efficient and well-known tools for assessment of voltage stability is modal analysis technique, which introduced by Gao et al. (1992), Kundur (1994) and Da Silva et al. (2004). Dong et al. (2005) proposed a Reactive Reserve Management Program (RRMP) based on an optimal power flow to manage critical reactive power reserves. Various generators were assigned different weights in order to maintain maximum reactive reserves within the areas that are most vulnerable to voltage instability problem. Affonso et al. (2004) presented a joint active/reactive power scheduling methodology that increases voltage stability margin using active participation factors derived from the modal analysis technique. Menezes et al. (2003, 2004) presented a one-day-ahead pre-dispatch scheduling methodology considering improvement of the voltage stability margin by scheduling of dynamic VAR sources. In their work modal analysis was done and active participation factors were used to define penalty factors for dynamic VAR sources, which are then incorporated to OPF formulation. Lin et al. (2003) presented an ORD methodology with consideration of the VSM as a constraint. Reactive power generation cost was minimized such that required VSM was satisfied through a unified OPF. Hosseinpour et al. (2008) proposed a combined operation of the Unified Power Quality Conditioner (UPQC) with wind power generation system considering investment cost.
This study presents a methodology for the inclusion of evaluation and improvement of voltage stability margin by optimizing the reactive power injections of generators and synchronous condensers. The objective is to maximize voltage stability margin maintaining the economical dispatch of active power by using Generator Participation Factors (GPFs) derived from the critical eigenvalue of the reduced Jacobian matrix. GPFs define penalty indices for all generators reactive injections, which are then added to the Optimal Power Flow (OPF) objective function as weighting factors, to obtain the most adequate reactive power injection for each generator or synchronous condenser. Generators reactive power injections are in proportional to their participation factors. These weighting factors cause that generators with high participations in critical mode of voltage (corresponding to critical eigenvalue of reduced Jacobian matrix) generate more reactive power support. As a result, the VSM will be improved with no negative impact on the active economical dispatch. The main contribution of this study is to use GPFs in the ORD problem. The problem formulated as an optimization problem. This optimization problem is a Non Linear Programming (NLP), which is solved using optimization toolbox of MATLAB software.
The results obtained for the IEEE 30-bus test system are presented to show that the proposed methodology leads to a significant improvement in the VSM of power systems.
Voltage stability is the ability of a power system to maintain steadily acceptable bus voltage at all buses under normal operating condition, after load increase or when the system is being subjected to disturbance. Voltage stability margin represents the distance, in MW or percentage, from the base case operation point to the maximum power transfer capability point of the system (PV curve nose point). For each load increase a load flow problem is solved and the set of obtained equilibrium points defines the PV curve. In this work, PV curves are obtained by considering load increases for all load buses in a proportional way to the base case loading (keeping constant power factor). System generation level is also increased in order to match the load increases during the PV curve construction process.
MATERIALS AND METHODS
Modal analysis for voltage stability assessment: Modal analysis technique identifies critical areas of voltage stability and provides information about the best actions to be taken for the improvement of system stability margins. GPFs indicate which of the dynamic VAR sources should inject more reactive power to improve the VSM and which of them should inject less. The linearized power-flow equations of a general power system are given by:
(1) |
Where:
| ΔP | = | Vector of bus active power injection variations |
| ΔQ | = | Vector of bus reactive power injection variations |
| Δθ | = | Vector of bus angle variations |
| ΔV | = | vector of bus voltage magnitude variations |
System voltage stability is affected by both P and Q. However, at each operating point we keep P constant and evaluate voltage stability by considering the relationship between Q and V (Gao et al., 1992; Kundur, 1994). By assuming:
(2) |
Where:
(3) |
where, JRQV is called the reduced Jacobian matrix of the system, which directly relates the bus voltage magnitude and bus reactive power injection. Voltage stability characteristics of the system can be identified by computing the eigenvalues and eigenvectors of JRQV. Let:
(4) |
Where:
| ξ | = | Right eigenvector matrix of JRQV |
| η | = | Left eigenvector matrix of JRQV |
| Λ | = | Diagonal eigenvalue matrix of JRQV |
(5) |
Or,
(6) |
where, ξi is the ith right eigenvector, ηi is the ith left eigenvector and λi is the ith eigenvalue of JRQV.
Since ξ-1 = η, Eq. 5 may be written as:
(7) |
Where:
| v = ηxΔV | = | The vector of modal voltage variations |
| q = ηxΔQ | = | The vector of modal reactive power variations |
Assuming that ith mode, the vector of modal reactive power variations (q) has all elements equal to zero except for the ith, which equals to 1. The corresponding vector of bus reactive power variations is:
(8) |
With the vector of bus reactive power variations equal to ΔQi, the vector of bus voltage variations, ΔVi is:
(9) |
And the corresponding vector of bus angle variation for ith mode, is:
(10) |
The relative participation of machine m in mode i is given by the generator participation factor (Gao et al., 1992; Kundur, 1994):
(11) |
where, NG is the number of generator buses.
The expression for Q at any bus k, is given by:
(12) |
where, the ![]() is the kj-th element of admittance matrix (Ybus).
is the kj-th element of admittance matrix (Ybus).
For PV buses, Eq. 12 could be linearized as below:
(13) |
Where:
(14) |
(15) |
where, NPQ is the number of PQ buses.
Using Eq. 9-10 and 13, it could be written for ith mode:
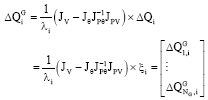 | (16) |
Substituting Eq. 8 in 16 the participation factor of machine m in mode i, I, GPFm,i, can be:
(17) |
Generator participation factors indicate, for each mode, which generator supply the most reactive power in response to an incremental change in system reactive loading. Generator participations provide important information regarding proper distribution of reactive reserve among all the machines in order to maintain an adequate voltage stability margin. Generators with high GPFi are important in maintaining stability of mode i (Gao et al., 1992; Kundur, 1994).
Proposed approach: The proposed MVAR (Mega Volt Ampere Reactive) scheduling method is based on two main steps: The first step obtains weight (or penalty) factors using modal analysis technique and the second step is the ORD, which is used to determine the desired reactive dispatch. The proposed methodology is shown in Fig. 1 and its main steps are the following.
Determination of desired penalty factors for dynamic VAR re-scheduling: Present method maximizes the VSM directly based on GPFs. It can be defined as a reactive power re-scheduling process and is solved by adding a penalty term on the OPF objective function. Generators with greater GPFs should inject more reactive power support, because their impact on VSM is more than the other dynamic VAR sources. The penalty (or weighting) factor is related with the machine reactive power impact on VSM and it is updated from the modal analysis, as follows:
| • | At iteration k, calculate the generator participation factors corresponding to the least stable mode from Eq. 17 |
| • | Through it, build the vector d (it gives the direction for changing the machines reactive injection) |
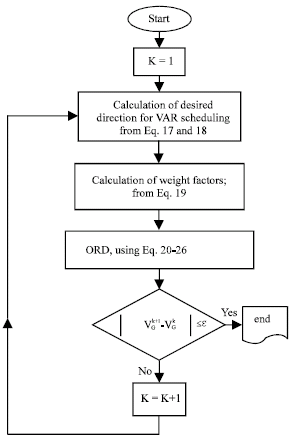 | |
| Fig. 1: | Reactive power rescheduling methodology |
(18) |
| • | Compute penalty factors as below: |
(19) |
where, α is a controlled step size (Tlelo-Cuautle et al., 2007). Generators with grater GPFs have smaller penalty factors, due to their more effectiveness on VSM. Therefore, these generators will inject more reactive power support and then, the VSM of the system will improve.
Optimal reactive-power dispatch (ORD): By adding a penalty factor for each machine reactive injection at the OPF objective function, it is possible to find the most adequate MVAR distribution to improve the VSM. Generators with high GPFs are important in maintaining stability of the least stable mode. Thus at each iteration it is necessary to identify the least stable mode (through calculation of the smallest eigenvalue of JRQV) and then calculate the corresponding penalty factors from Eq. 18 and 19. The OPF model, which is used in this study, is as follows.
Objective function: In this ORD problem it is assumed that active power generations are fixed and re-scheduling is carried out on reactive power generations. Thus the objective function could be written, as following:
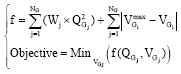 | (20) |
where, QGj and VGj is reactive power generation and voltage of jth reactive power source.
Constraints: The details of the OPF constraints are discussed here (Zhang et al., 2007):
| • | Power flow constraints: |
(21) |
(22) |
| • | Variable limits: |
(23) |
(24) |
(25) |
(26) |
Where:
| Pgi | = | Generator active power output |
| PLi | = | Load active power |
| QGi | = | Generator reactive power output |
| QLi | = | Load reactive power |
| VGi | = | PV bus voltage |
| VLi | = | Bus voltage |
| θi | = | Bus voltage angle |
| = | Transmission line flow |
In order to evaluate the suitability of the proposed methodology, VSM is calculated using Fig. 2, as follows:
(27) |
where, Pinitial and Pmax represent the active power loads at current operating point and PV curve nose point, respectively and:
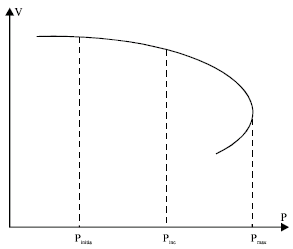 | |
| Fig. 2: | PV curves |
(28) |
(29) |
Also, the loading factor is defined as
(30) |
RESULTS AND DISCUSSION
The proposed ORD methodology is tested on the IEEE 30-bus test system, which has 6 generators and 41 transmission lines. The configuration of the power system is shown in Fig. 3. For this test system α = 10, is suitable. As mentioned previously, the problem formulated as an optimization problem, which is a Non Linear Programming (NLP). Using optimization toolbox of MATLAB software and some programming, this NLP is solved. BFGS Quasi-Newton algorithm is employed for the optimization. Present optimization problem is a problem with continues (non integer) variables and this algorithm is suitable for NLP with continuous variables.
Active power injections of the generators are fixed for the initial solution, except for the slack bus. The relationship between VAR source 4 (at bus 8) output VAR and its GPF, is shown in Fig. 4. Figure 4 shows that the scheduling of VAR source is in direction of its GPF. The initial and final (after optimization) PV curves for buses 20 and 30 are shown in Fig. 5. From Fig. 5, it can be found that the voltage profile has improved for any loading factor and eventually, voltage stability margin has been increased significantly.
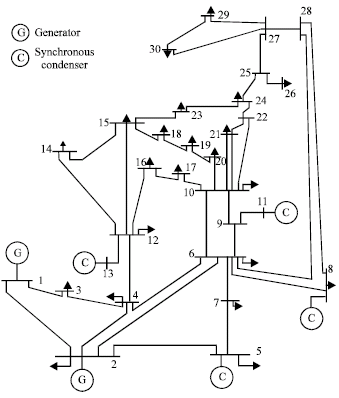 | |
| Fig. 3: | IEEE 30-bus test system |
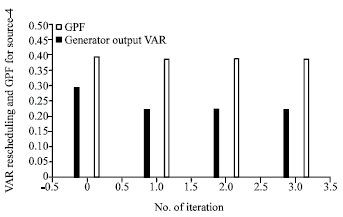 | |
| Fig. 4: | VAR rescheduling and GPF for source-4 (at bus 8) |
The effect is rather significant since the ORD is applied without adding new VAR sources and the active power dispatch is not changed. Figure 6 shows the total active and reactive losses of the system, during re-scheduling process. It could be seen that the active and reactive losses are decreased.
In the voltage stability problem, the reactive reserve margin is extremely important at generators, because it gives an advance indication of how close the generator to its operation limits. Figure 7 shows the modified reactive power injections of VAR sources at each iteration of the proposed algorithm. It can be observed that unless VAR source 6 (at bus 13), reactive power injections of all other sources decreased.
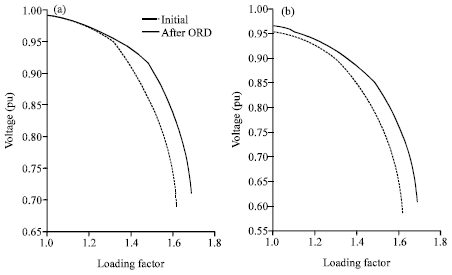 | |
| Fig. 5: | Initial and final PV curves (a)for bus 20 and (b) for bus 30 |
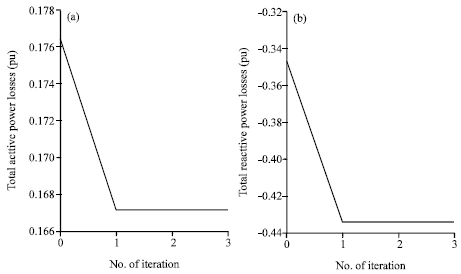 | |
| Fig. 6: | Initial and final PV curves (a)for bus 20 and (b) for bus 30 |
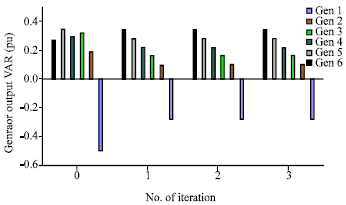 | |
| Fig. 7: | Reactive power injections of generators |
Therefore, the reactive reserve of system is increased. Figure 8 justifies this conclusion and illustrates that the total reactive power generation of the system is decreased. The increase of reactive reserve of system indirectly increases the VSM.
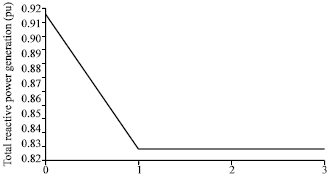 | |
| Fig. 8: | Total reactive power generation |
The numerical values of Pinitial, Pmax and VSM corresponding to the figures are given in Table 1.
| Table 1: | Numerical values for voltage stability analysis |
 | |
As it is observed, the VSM is increased 6.90%, which is significant, because no modification is done on generators active-power dispatch.
CONCLUSION
This study discusses the management of dynamic reactive power generation in order to improve voltage stability margin. The method is based on optimal power flow. The management of the VAR generation is processed as an optimization problem.
Generator participation factors is introduced and then incorporated to ORD problem. This study has shown that the generator participation factors are adequate for the indication of the direction of change of reactive power injection of dynamic VAR sources, in order to increase the voltage stability margin. The method studied has proved efficient in improving voltage stability margins by modifying the reactive generation of dynamic VAR sources. By applying the proposed ORD approach, the reactive power reserves in the system increase and active and reactive power losses decrease. The voltage stability margin has been improved without adding new VAR sources and changing the active power dispatch and consequently the cost of generation.
REFERENCES
- Affonso C.A., L.C. da Silva, F.G.M. Lima and S. Soares, 2004. MW and Mvar management on supply and demand side for meeting voltage stability margin criteria. IEEE Trans. Power Syst., 19: 1538-1545.
Direct Link - Da Silva, L.C.P., Y. Wang, V.F. da Costa and W. Xu, 2004. Assessment of generator impact on system power transfer capability using modal participation factors. IEE Proc. Generat. Transmiss. Distribut., 149: 564-570.
Direct Link - Dong, F., B.H. Chowdhury, M.L Crow and L. Acer, 2005. Improving voltage stability by reactive power reserve management. IEEE Trans. Power Syst., 20: 338-345.
Direct Link - Esmin, A.A., G. Lambert-Torres and A.C.Z.D. Souza, 2005. A hybrid particle swarm optimization applied to loss power minimization. IEEE Trans. Power Syst., 20: 859-866.
Direct Link - Gao, B., G.K. Morison and P. Kundur, 1992. Voltage stability evaluation using modal analysis. IEEE Trans. Power Syst., 7: 1529-1542.
Direct Link - Lin, X., A.K. David and C.W. Yu, 2003. Reactive power optimization with voltage stability consideration in power market systems. IEE Proc. Generat. Transmiss. Distribut., 150: 305-310.
Direct Link - Menezes, T., L.C.P. da Silva and V.F. da Costa, 2003. Dynamic VAR sources scheduling for improving voltage stability margin. IEEE Trans. Power Syst., 18: 969-971.
Direct Link - Menezes, T., L.C.P. da Silva and V.F. da Costa, 2004. MVar management on the pre-dispatch problem for improving voltage stability margin. IEE Proc. Generat. Transmiss. Distribut., 151: 665-672.
Direct Link - Venkatesh, B., G. Sadasivam and M. Abdullah Khan, 2000. A New optimal reactive power scheduling method for loss minimization and voltage stability margin maximization using successive multi-objective fuzzy LP technique. IEEE Trans. Power Syst., 15: 844-851.
CrossRef - Yan, W., F. Liu, C.Y. Chung and K.P. Wong, 2006. A hybrid genetic algorithm-interior point method for optimal reactive power flow. IEEE Trans. Power Syst., 21: 1163-1169.
CrossRef - Zhang, W., F. Li and L.M. Tolbert, 2007. Review of reactive power planning: Objectives, constraints and algorithms. IEEE Trans. Power Syst., 22: 2177-2186.
CrossRef - Tlelo-Cuautle, E. and J.M. Mu�oz-Pacheco, 2007. Simulation of Chua's circuit by automatic control of step-size. Applied Math. Comput., 190: 1526-1533.
CrossRefDirect Link - Hooshmand, R.A., 2008. Optimal design of load shedding and generation reallocation in power systems using fuzzy particle swarm optimization algorithm. J. Applied Sci., 8: 2788-2800.
CrossRefDirect Link - Hosseinpour, M., A. Yazdian, M. Mohamadian and J. Kazempour, 2008. Design and simulation of UPQC to improve power quality and transfer wind energy to grid. J. Applied Sci., 8: 3770-3782.
CrossRefDirect Link - Zhao, B., C.X. Guo and Y.J. Cao, 2005. A multiagent based particle swarm optimization approach for optimal reactive power dispatch. IEEE Trans. Power Syst., 20: 1070-1078.
CrossRef








