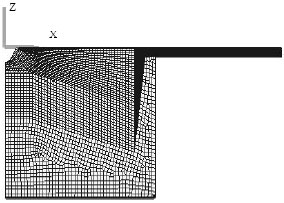
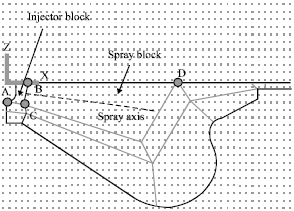
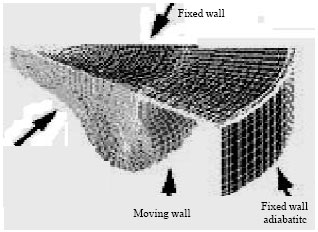
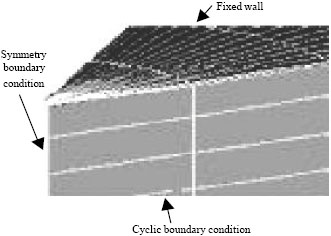
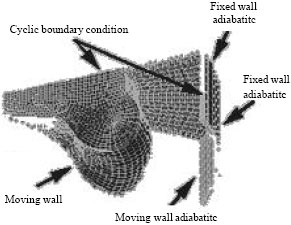
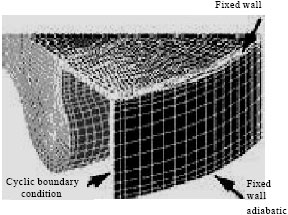
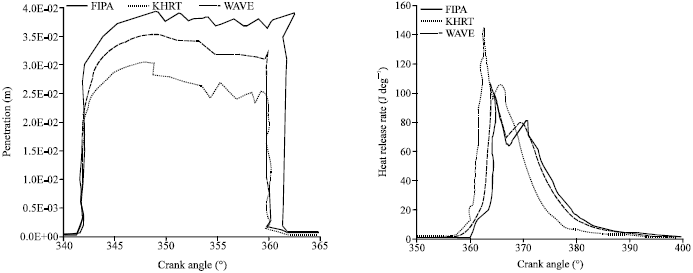
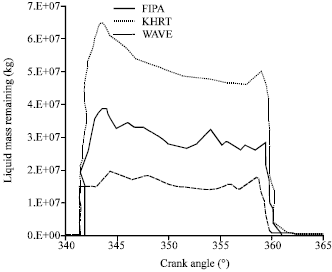
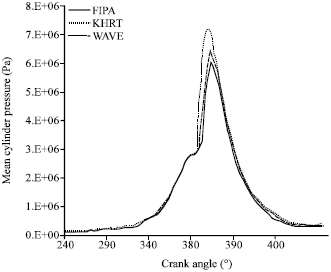
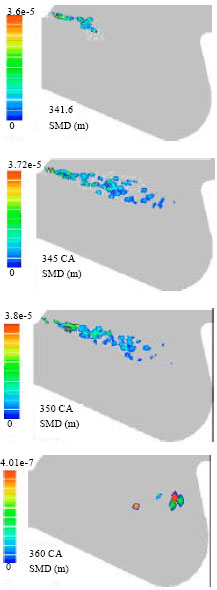
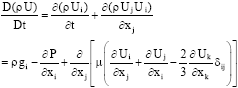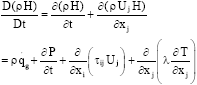Research Article
Investigation of Jet Break-Up Process in Diesel Engine Spray Modelling
Department of Mechanical Engineering, Ferdowsi University of Mashhad, Mashhad, Iran
A. Ghasemi
Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran