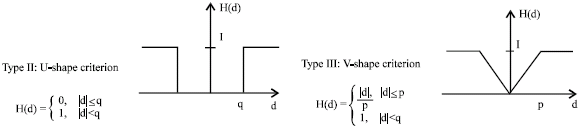
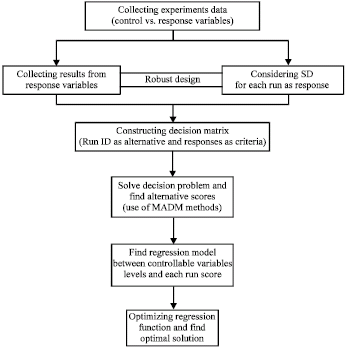
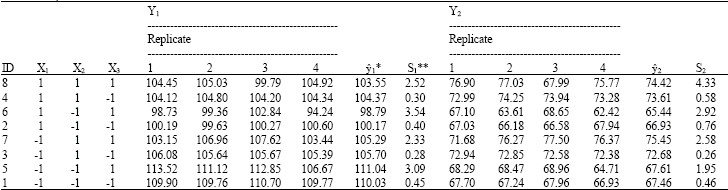
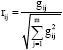Research Article
An Extension of Multi-Response Optimization in MADM View
Department of Industrial Engineering, Faculty of Engineering, Shahed University, P.O. Box 18155/159, Tehran, Iran
T.H. Hejazi
Department of Industrial Engineering, Shahed University, Tehran, Iran