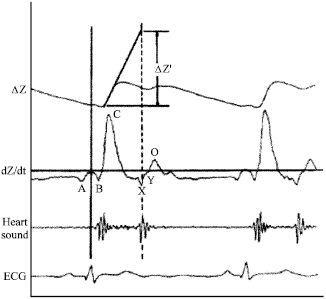
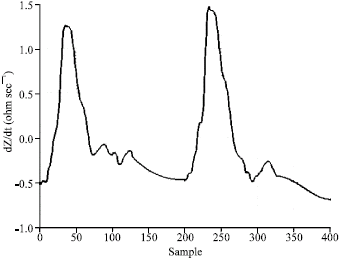
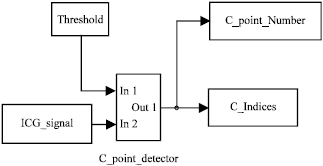
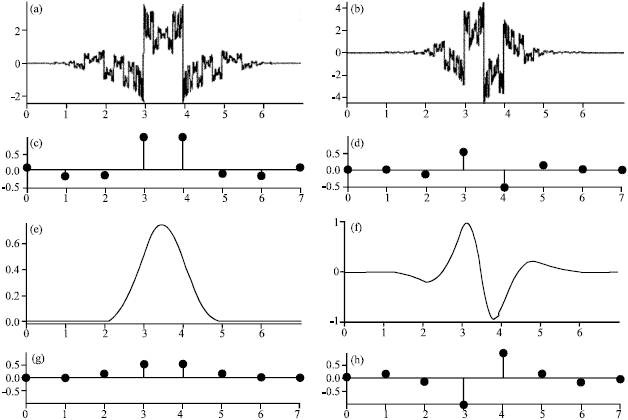
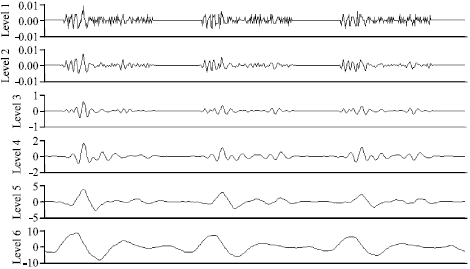
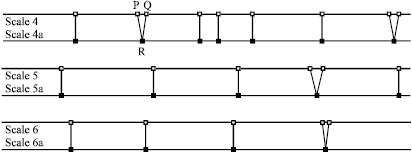
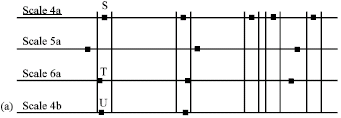
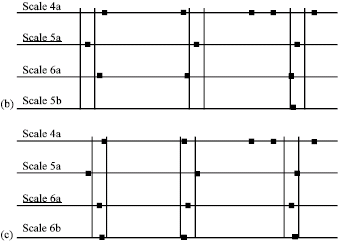
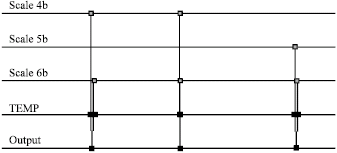
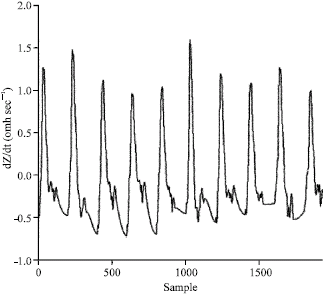
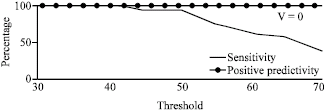
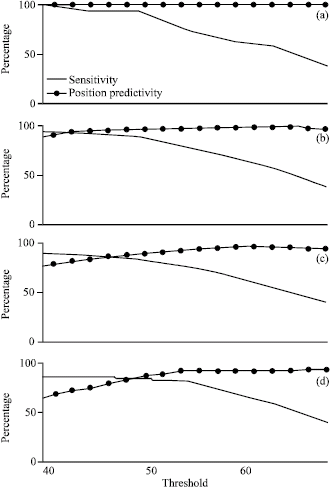
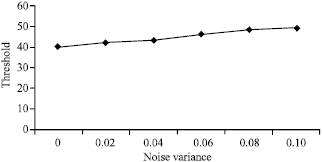
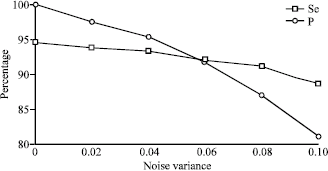
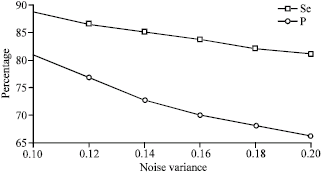
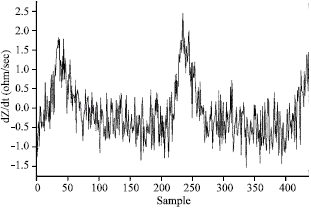
Research Article
High Sensitivity and Noise Immune Method to Detect Impedance Cardiography Characteristic Points Using Wavelet Transform
Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari via E. Orabona, 4-70125 Bari, Italy
Matteo D�Aloia
Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari via E. Orabona, 4-70125 Bari, Italy
Beniamino Castagnolo
Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari via E. Orabona, 4-70125 Bari, Italy