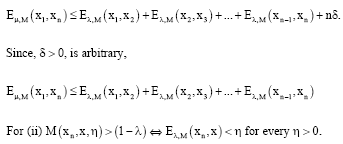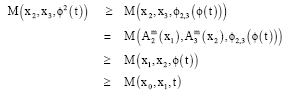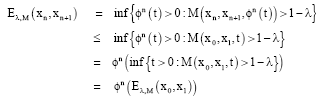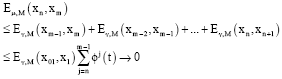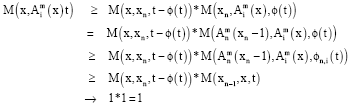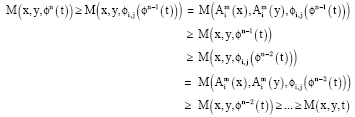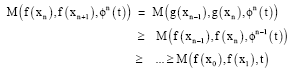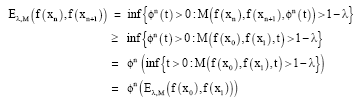Research Article
Nonlinear Contraction Theorems in Fuzzy Spaces
Islamic Azad University, Aiatollah Amoli Branch, Amol 678, Iran
R. Saadati
Islamic Azad University, Aiatollah Amoli Branch, Amol 678, Iran
A. Shahmari
Islamic Azad University, Aiatollah Amoli Branch, Amol 678, Iran
S.M. Vaezpour
Department of Mathematics and Computer Science, Amirkabir University of Technology, 424 Hafez Avenue, Tehran 15914, Iran