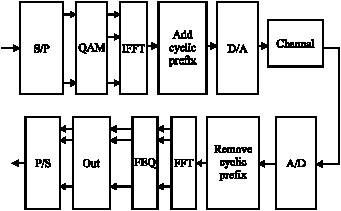
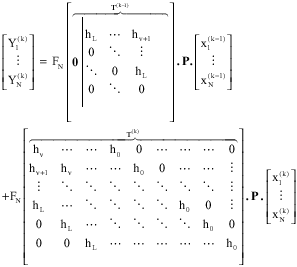
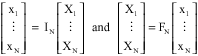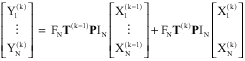Research Article
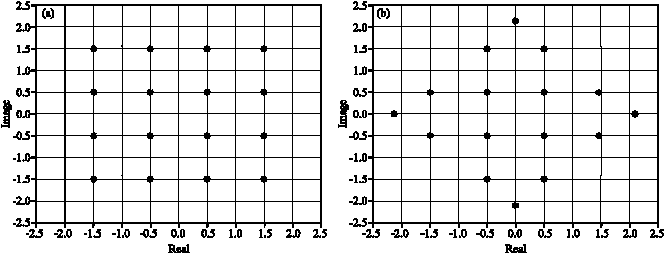
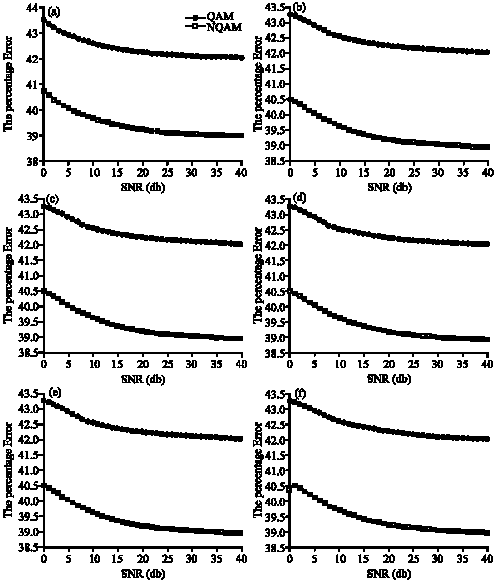
A Novel Constellation with Different Noises in Discrete Multitone System
Department of Electrical, Science and Research Branch, Islamic Azad University, Tehran, Iran
M. Lotfizad
Department of Electrical and Computer Engineering, Tarbiat Modarres University, Tehran, Iran
M. Ghanbari
Department of Electronic Systems Engineering, University of Essex, Cochester, UK