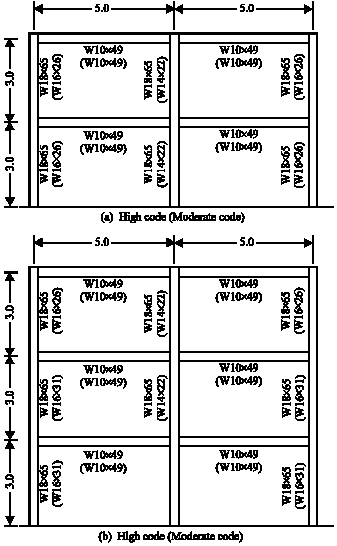
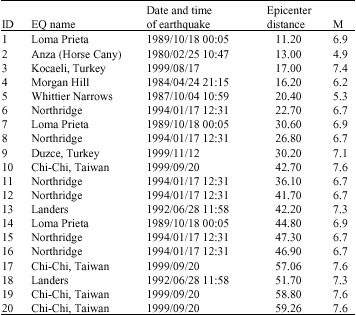
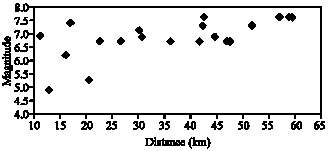
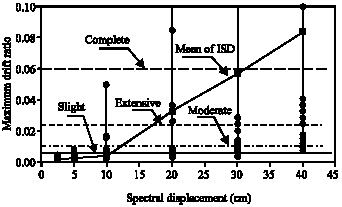
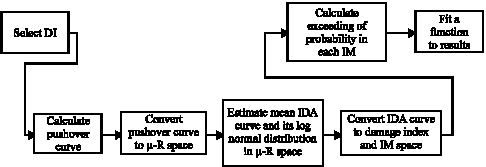
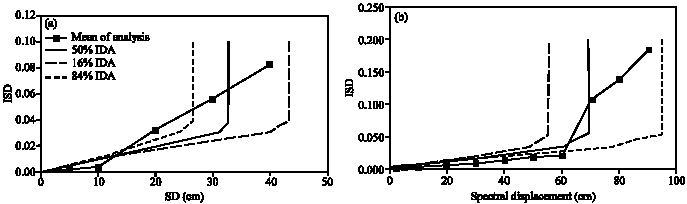
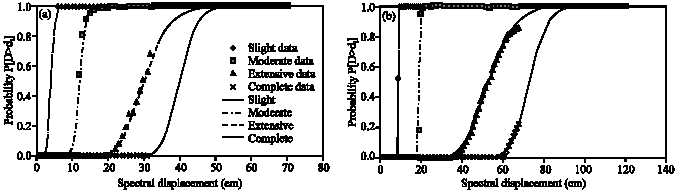
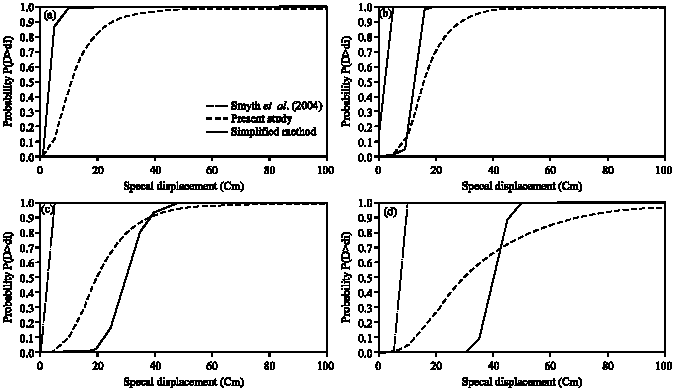
Research Article
Developing Seismic Fragility Function of Structures by Stochastic Approach
International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran
M. Ghafory-Ashtiany
International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran
S. Eshghi
International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran
M.R. Zolfaghari
International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran