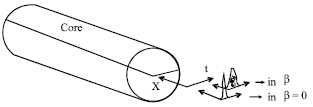
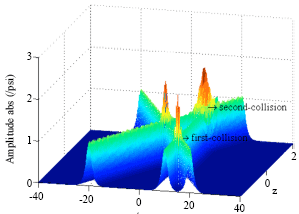
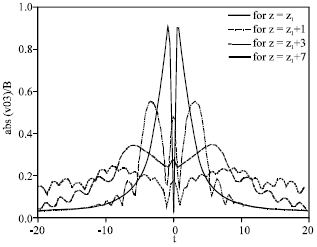
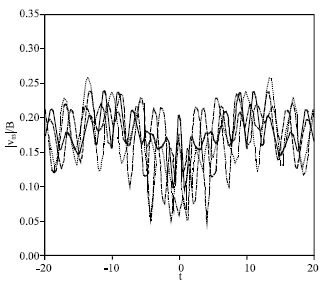
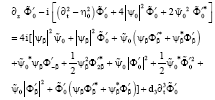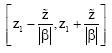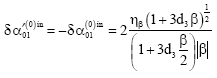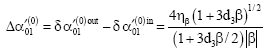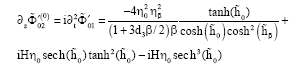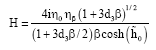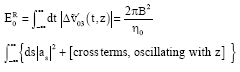Research Article
Inelastic Collision of Optical Solitons
Department of Physics, University of Guilan, P.O. Box 1914, Rasht, Iran
S. Batebi
Department of Physics, University of Guilan, P.O. Box 1914, Rasht, Iran
H. Rahimpour Soleimani
Department of Physics, University of Guilan, P.O. Box 1914, Rasht, Iran