Research Article
Finite Element Modeling of Leaching from a Municipal Landfill
Department of Civil Engineering, Khajeh Nasir University of Technology, Tehran, Iran
H.R. Kazemi Esfeh
Department of Civil Engineering, Shiraz University, Shiraz, Iran
Leachate from Sanitary landfills is recognized as important groundwater pollutants. The contaminants are released from the refuse to the passing water by physical, chemical and microbial processes and percolate through the unsaturated environment, polluting the groundwater with organic and inorganic matter. If allowed to migrate freely from the landfill, leachates may pose a serve pollution threat to groundwater (Demetracopoulos, 1986).
The modeling of leachate generation hinges on an understanding of the mechanisms of mass release from the solid to the liquid phase and contaminant decay. These mechanisms are influenced by such factors as climatic conditions, type of waste, site geohydrologic conditions and chemical reactions as well as microbial decomposition of organic matter (Demetracopoulos, 1986). McCreanor and Reinhart (2000) developed a mathematical for the leachate of landfill in the United States. The contaminant plume transport model was presented by Aroa et al. (2007). Khire and Mukherjee (2007) have done an extensive research on leachate injection using vertical wells in bioreactor landfills.
The mathematical simulation of landfill leachate generation and transport is addressed in the present study. The mechanisms controlling generation and transport are incorporated in the appropriate governing equations and a finite element solution is presented. Accuracy of Model has been shown by comparison of results by experimental measurements.
EXPERIMENTAL WORK
Many empirical investigations have been made into the process of landfill leaching and stabilization. The goals of leachate generation studies have been to determine the volume and rate of leachate production, identify the types and concentration histories of pollutants present in leachate and to observe relationships among climate, age, refuse placement, leachate production, gas production, temperature, settlement and overall landfill stabilization. Several studies have utilized laboratory-scale columns filled with compacted municipal refuse (Qasim and Burchinal, 1970; Fungaroli, 1971; Rovers and Farquhar, 1973; Walsh and Kinman, 1979; Wigh and Brunner, 1979; Scarpino and Donelly, 1979; Report To Congress, 1977). Others have investigated the behavior of pilot or field-scale landfills ranging from 0.9-4.7 m2 (Hentrich et al., 1979; Wigh, 1979; Leckie et al., 1979). The behavior of experimental landfills operated with leachate recalculation has been reported (Birbeck et al., 1980; Leckie et al., 1979; Pohland et al., 1979; Pohland, 1975). A summery of reported empirical investigation has been prepared (Straub, 1980a).
The methodologies incorporated in these studies have been similar. An input/output approach is typical. Inputs to the experimental landfill, namely municipal solid waste, additives and moisture were controlled or measured or both. Liquid and gaseous outputs have been determined and analyzed. Refuse composition at various stages of landfill stabilization has been determined (Chain and Dewalle, 1976; Pohland, 1975). Little data have been gathered from the interior of experimental landfills, except far temperature and transport in the landfill interior have not been well documented.
Several similarities in the leachate behavior of the landfills may be generalized. In virtually all the experimental landfills, significant rates of leachate production were delayed from the initial application of moisture, although small, intermittent volumes of leachate may be produced prior to continuous leaching. Moisture balance on the landfill cells have indicated that after the commence of significant leachate production, the overall moisture content of the landfill remains essentially constant and leachate is collected at roughly a one-to-one proportion with net moisture application. These observation have led to the concept of refuse field capacity, defined fort porous medium as the average volumetric moisture content above which continuous gravity drainage of water from the medium will occur. Field capacities computed from input/output moisture data from various studies indicate different values among several experimental landfills, generally ranging between 0.3 and 0.4 cm/cm (Straub, 1980b).
High concentration of organic and inorganic contaminants are typically associated with leachate. Peak concentrations of cod and total solids above 50000 mg L-1 are common. However, wide ranges of concentrations of various contaminants have been observed for different landfills at various ages. Chain and Dewalle investigated the characteristic of leachate from 13 field and laboratory-scale landfills. While wide differences in leachate composition were noted, a meaningful qualitative comparison was made on the basis of landfill age, utilizing the ratios COD/TOC, BOD/COD, VS/FS and percentage of free volatile fatty acid carbon to TOC. They suggest a general decrease both in organic and inorganic leachate strength with age and characterize young landfills as having high strength leachate, while dilution and microbial utilization of organic reduce leachate strength from older landfills. The pattern of high contaminant concentration near the onset of leaching, followed by a general decrease, is typical among other investigations (Walsh and Kinman, l979; Phelps, 1988; Raveh, 1979; Scarpino and Donelly, 1979), although specific time rates of decrease vary considerably.
Although basic methodological similarities exist among experimental landfill studies, factors such as physical dimension of the landfills refuse composition, refuse placement and density, additives to refuse, initial moisture content, temperature and temperature control have varied greatly among the studies. The rate and pattern of moisture application also have varied. Natural moisture ranging from constant application to seasonal variation and average rates ranging from less than 0.1 to over 1.0 cm day-1. The time span of reported results ranges from several weeks to several year and as the specific objectives of the studies differ, the measured variables and the form in which results are reported have varied (Straub and Lynch, 1982).
LEACHATE MODELING
Fenn developed a method to estimate the time of first appearance of leachate and subsequent rates of leachate production. This procedure applies a water balance to estimate net moisture input to refuse from a soil cover and utilizes field capacity assumption to calculate refuse moisture retention and leachate production.
A semi-empirical equation was developed by Wigh to describe the concentration history of various contaminants in leachate generated from an experimental landfill. The equation is based on two consecutive first order reactions and expresses contaminant concentration as a function of cumulative leachate volume, maximum concentration and two rate constants. Parameters of the equation were evaluated to obtain good visual fit concentration histories of several contaminants. The model captures the general decrease from high initial concentration, which is typical of observed leachate behavior, but its depth, etc. Similarly, Raveb observed declining concentrations of various pollutants in leachate from experimental landfill column and described the concentration histories of various pollutants with an exponential function of time. Empirically fit parameters were evaluated for one set of experiments.
Qasim and Burchinal operated three experimental landfill columns of varying heights and applied column operation theory to describe the leaching of chloride. The concentration histories of 14 other contaminants were related to the chloride estimates, with reasonable agreement. The procedure relies on empirically derived parameters, but is responsive to depth of refuse and rate of moisture flow through the fill.
Phelps developed a model of sanitary landfill leaching utilizing mass transfer equations based on flow through a moisture film the refuse particles. The model is applied for assumptions of constant moisture infiltration rate and constant moisture content above a wetting front. Model predictions are compared with observed results from several experimental landfill columns which were subjected to various moisture application rates and contained refuse at different depths. Although the model requires the empirical estimation of several parameters and makes limiting assumptions about moisture flow, it is based on descriptions of fundamental mass transfer and contaminant transport processes (Straub and Lynch, 1982).
Straub and Lynch (1982) and Demetracopoulos (1986) performed a finite deference model for landfill leachate generation by using of convection-dispersion equation in unsaturated medium of a landfill.
MATHEMATICAL MODEL
Water flow model: For solving convection dispersion equation, water content and Darcy velocity is needed. These parameters are achieved by solving moisture transport Equation. In this study water content and Darcy velocity are obtain by using of LEACHW (Huston and Wagenet, 1989) model. Equations that use in this model are as follows:
Continuity equation:
(1) |
(2) |
Moisture transport equation:
(3) |
Parameters are defined as:
| θ | : | Water content [L3/L3] |
| q | : | Darcy velocity [L/T] |
| z | : | Elevation, computed from surface to bottom [L] |
| K(θ) | : | Hydraulic conductivity [L/T] |
| : | :Suction head [L] | |
| t | : | Time [T] |
| c | : | Specific moisture capacity equal to dθ/d θ - |
| If |
(4) |
(5) |
(6) |
(7) |
Parameters are defined as:
(8) |
(9) |
| : | Suction head near saturation [L] | |
| Ksat | : | Saturation hydraulic Conductivity [L/T] |
| b | : | An experimental constant |
| θs | : | Water content [L3/L3] |
Contaminant transport through the landfill is controlled by the bulk motion of the fluid and mechanical dispersion. Mixing due to molecular diffusion is negligible compare to that caused by dispersion. Because of discussing contaminant is inorganic total solids, decay not exists. The mass transport equation is derived by applying continuity on an infinitesimal control volume (Strub and Lynch, 1982):
(10) |
(11) |
(12) |
| C | : | Fluid phase concentration [M/l3] |
| Dk | : | Hydrodynamic longitudinal dispersion coefficient [L2/T] |
| λ | : | Dispersivity [L] |
| K’ | : | A rate coefficient [1/T] |
| S | : | Local mass per bulk volume of refuse available for transfer at time t [M/T3] |
| S0 | : | Local mass per bulk volume of refuse available for transfer at time t = 0 [M/T3] |
| Cst | : | Maximum contaminant concentration in the liquid phase [M/T3] |
FINITE ELEMENT SOLUTION
In this finite element solution two nodes one dimensional elements are used (Fig. 1). The Shape functions are as follows:
(13) |
The weak form of contaminant transport is:
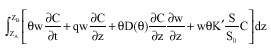 | (14) |
(15) |
where, ZA and ZB are coordinates of start and end node of a typical element and w is trial function.
Approximation of solution is assumed as:
(16) |
If w = Ni (ξ) then
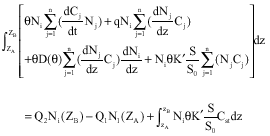 | (17) |
(18) |
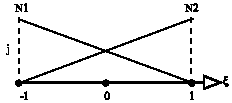 | |
| Fig. 1: | One dimensional master element and shape functions |
(19) |
(20) |
(21) |
(22) |
(23) |
(24) |
| Δt | = | Time step |
| K | = | Previous time |
| K+1 | = | Current time |
| K+1/2 | = | Interpolation between K and K+1 |
After assembling boundary condition has been applied. The upper boundary condition used here in is known concentration history.
(25) |
The lower boundary is considered here in as:
(26) |
Initial condition for this problem is:
(27) |
Because of nonlinearity of equation, a Picard method is used to solve system of equations.
MODEL VERIFICATION
For verifying model, two experimental measurements are used. The first is an experimental landfill that history of TS concentration at the bottom of landfill has been measured reported by Qasim and Burchinal (1970). Characteristic of experiment are as follow:
| Total time of simulation | : | 163 days |
| Length of landfill | : | 195 cm |
| Averaged pure precipitation | : | 0.544 cm day-1 |
The following parameters are assumed:
| Cst | : | 55000 mg L-1 |
| S0 | : | 37000 mg L-1 |
| λ | : | 5 cm |
| b | : | 7 |
| : | 100 cm | |
| Ksat | : | 0.544 cm day-1 |
A comparison between experimental measurement and model simulation is shown in Fig 2.
The model is run for two value of initial concentration but finally both of TS Cures are converges together and experimental result. As one can see the difference between the experimental and simulated data shows that initially is high, but as the time increase, the difference becomes minor. The data from Qasim and Burchinal has used for the verification of the model because of the simulation between their work and the present work which is Shiraz Landfill.
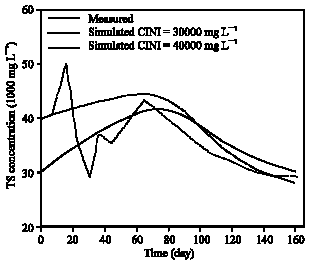
The second is a long time experimental landfill. The leachate total solids concentration from the Center Hill, Test Cell#4, as reported by Walsh and Kimnan (1979), was simulated with the model. Characteristics of experiment are as follows:
| Total time of simulation | : | 1000 days |
| Length of landfill | : | 240 cm |
| Averaged pure precipitation | : | 0.223 cm day-1 |
The following parameters are assumed:
| Cst | : | 55000 mg L-1 |
| S0 | : | 30000 mg L-1 |
| λ | : | 5 cm |
| b | : | 7 |
| : | 100 cm | |
| Ksat | : | 0.223 cm day-1 |
 | |
| Fig. 2: | History of computed and measured bottom TS concentration |
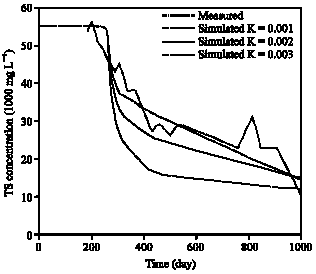 | |
| Fig. 3: | History of computed and measured bottom TS concentration |
A comparison between experimental measurement and model simulation is shown in (Fig. 3). The model has been run for averaged rate of daily precipitation, therefore no local picks bas been seen in the curve. The peaks in the curve are due to the seasonal changes for irrigation application rate.
Model has been run for three value of K’ that K’ have the best result.
A comparison between Demetracopoulos (1986) example and model has been prepared. Characteristics of example are as follows:
| Total time of simulation | : | 1410 days |
| Length of landfill | : | 610 cm |
| Averaged pure precipitation | : | 0.213 cm day-1 |
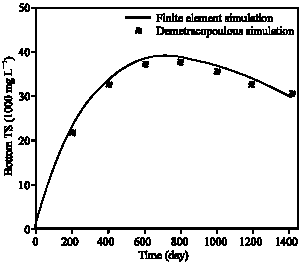 | |
| Fig. 4: | History of Demetracopoulos (1986) and this model simulation bottom TS concentration |
The following parameters are assumed:
| Cst | : | 45000 mg L-1 |
| S0 | : | 45000 mg L-1 |
| λ | : | 2.3 cm |
| b | : | 7 |
| : | 35 cm | |
| Ksat | : | 0.0018 cm day-1 |
Demetracopoulos (1986) results and model simulation is shown in Fig. 4. There are good agreements between Demetracopoulos simulation results and present model ones. The main reason for the agreements between simulation results by the present model with Demetracopoulos is that the chloride is a conservative material with no sources and sinks in the model.
A mathematical model describing generation and transport contaminants through a solid waste landfill was formulated and solved numerically by the finite element method.
The result of model has been compared with two experimental works.
The preceding results demonstrate the feasibility of analyzing compacted solid waste as an unsaturated porous medium. The advantage of this analytical approach lies in its process orientation leachate quantity and quality results from the interaction of fundamental transport phenomena within specific physical and environmental setting. At present, leachate model is appropriate primarily for research purposes, insofar as they provide organized analytical structures for the design and interpretation of experiments. Simulation obtain with preliminary, aggregate representations of major hydraulic and contaminant transport processes are overall agreement with leachate data documented in separate studies. Additional experimental work is required in order to identify and refine the description of basic processes occurring in the landfill environment. Result of short time experimental landfill works can’t be a good approximation of contaminant transport terms and long term study is needed. Value of initial concentration is an important parameter only in primary times and after a long time period effect of initial concentration has been omitted.
K’ is a very important term in contaminant transport equation in a landfill and a good value of K’ is obtain by several long times experimental works on landfill samples. Ultimately, porous medium-based landfill models could be applied to field-scale problems, although it must be recognized that such applications would require extensive empirical support.