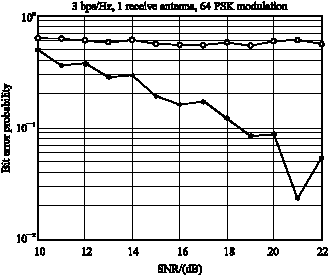
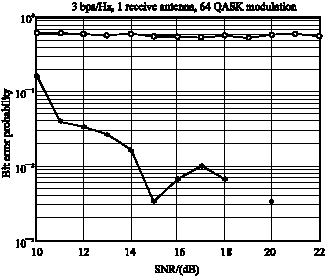
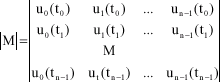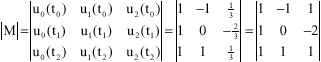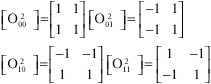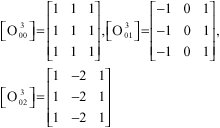Research Article
Maximam Diversity and Full Rank Space-Time Block Code Based on Orthogonal Polynomials
Department of Computer Science and Engineering, Annamalai University, Annamalainagar- 608 002, India
K. Selvakumar
Department of Computer Science and Engineering, Annamalai University, Annamalainagar- 608 002, India