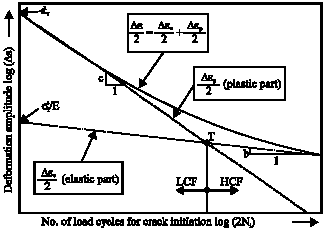
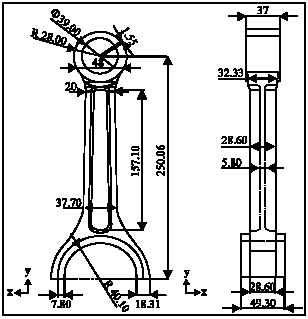
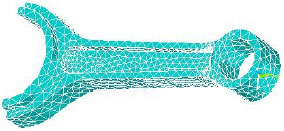
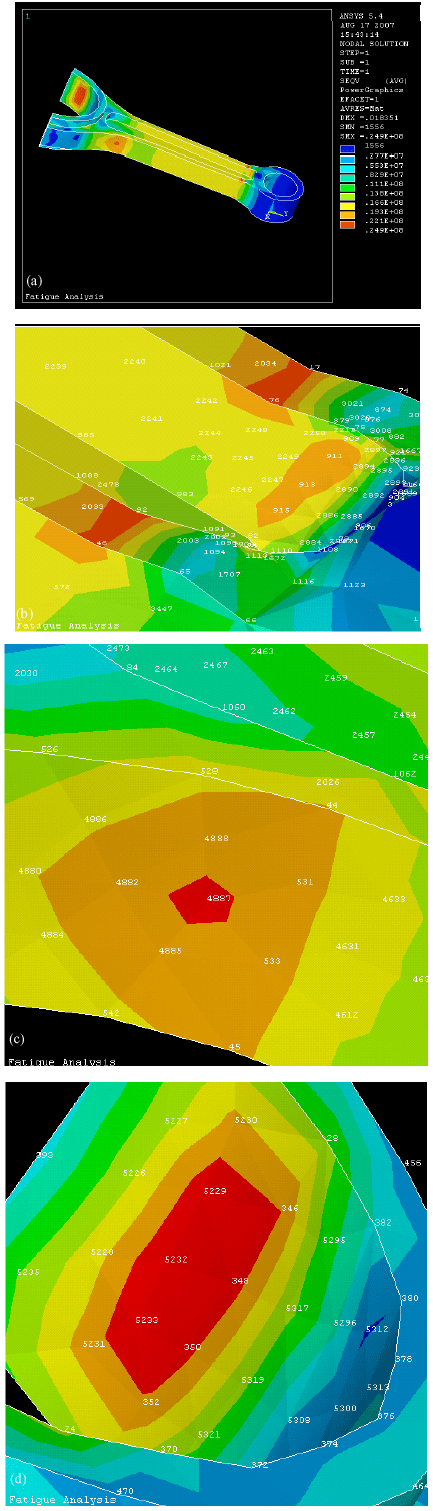
Research Article
Fatigue Analysis of Connecting Rod of U650 Tractor in the Finite Element Code ANSYS
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran
S.S. Mohtasebi
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran
S.A. Mireei
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran
E. Mahmoodi
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran