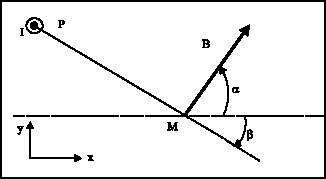
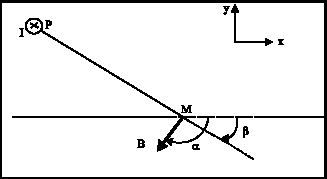
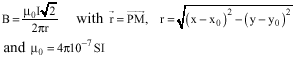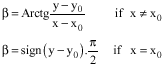Research Article
Determination of the Distance Security from Overhead Electric Lines
Department of Electrical and Electronic Engineering, Institut National Polytechnique Houphouët-Boigny (INP-HB), BP 1093 Yamoussoukro, Côte d`Ivoire
M. Koffi
Department of Electrical and Electronic Engineering, Institut National Polytechnique Houphouët-Boigny (INP-HB), BP 1093 Yamoussoukro, Côte d`Ivoire
M.A. Kouacou
Department of Electrical and Electronic Engineering, Institut National Polytechnique Houphouët-Boigny (INP-HB), BP 1093 Yamoussoukro, Côte d`Ivoire
O. Asseu
Department of Electrical and Electronic Engineering, Institut National Polytechnique Houphouët-Boigny (INP-HB), BP 1093 Yamoussoukro, Côte d`Ivoire
A. Tanoh
Department of Electrical and Electronic Engineering, Institut National Polytechnique Houphouët-Boigny (INP-HB), BP 1093 Yamoussoukro, Côte d`Ivoire
D. Konan
Department of Electrical and Electronic Engineering, Institut National Polytechnique Houphouët-Boigny (INP-HB), BP 1093 Yamoussoukro, Côte d`Ivoire