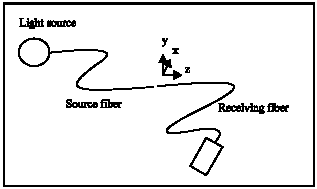
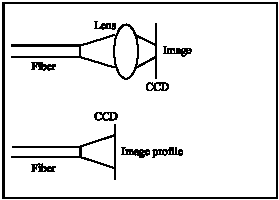
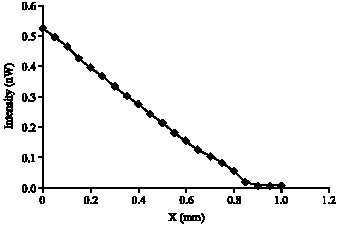
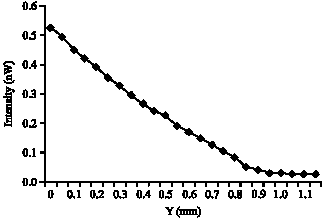
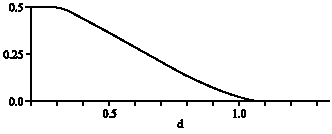
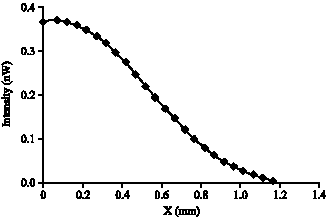
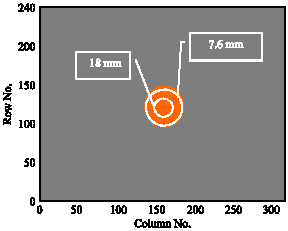
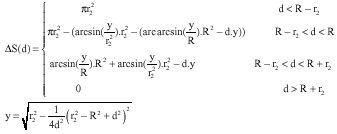Research Article
Beam Profile and Image Transfer Study in Multimode Optical Fiber Coupling
Plasma Physics Research Center, Islamic Azad University,P.O. Box 14665-678, Tehran, Iran
H. Golnabi
Institute of Water and Energy, Sharif University of Technology, P.O. Box 11365-8639, Tehran, Iran