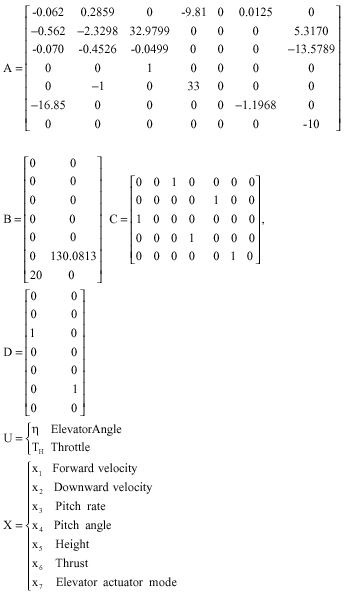
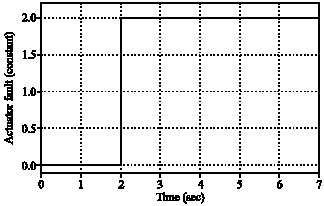
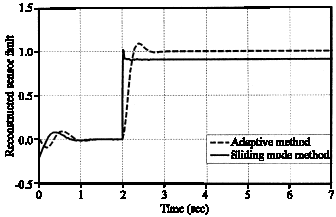
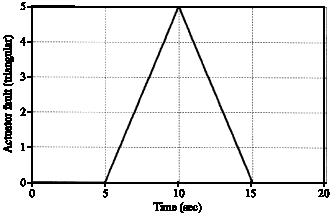
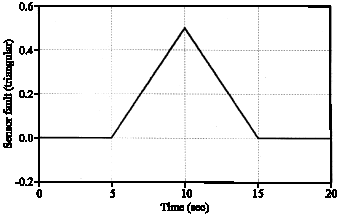
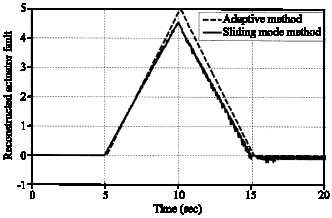
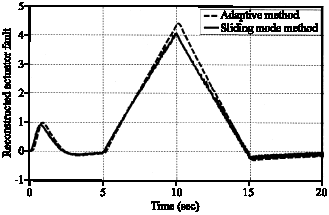
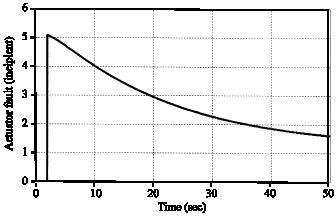
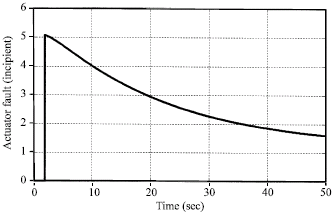
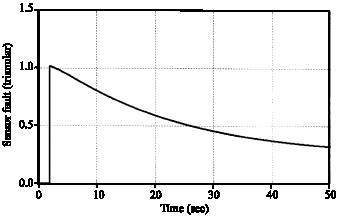
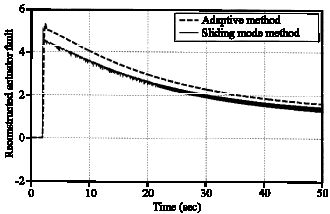
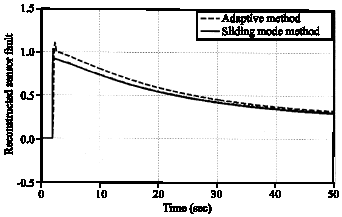
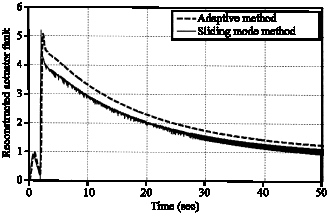
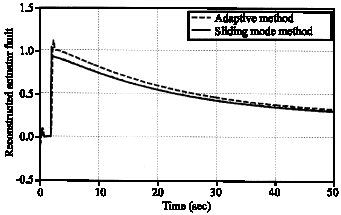
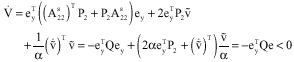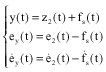Research Article
Fault Diagnosis Using Adaptive Technique
Shahrood University of Technology, Postal Code 3619995161, P.O. Box 317, Shahrood, Iran
M.A. Sadrnia
Shahrood University of Technology, Postal Code 3619995161, P.O. Box 317, Shahrood, Iran
A. Darabi
Shahrood University of Technology, Postal Code 3619995161, P.O. Box 317, Shahrood, Iran