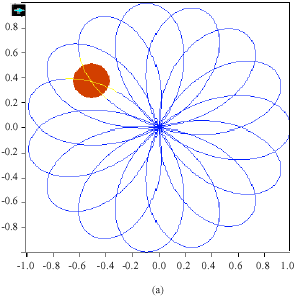
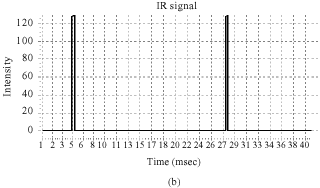
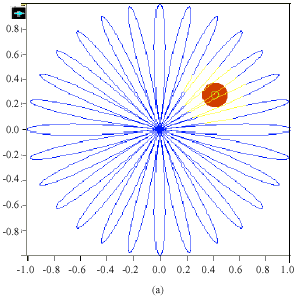
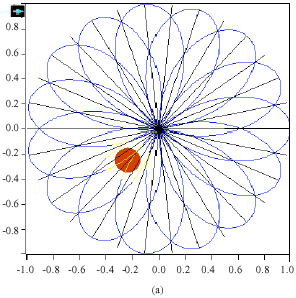
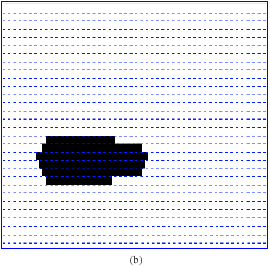
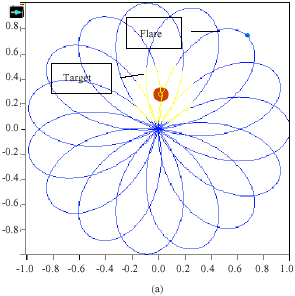
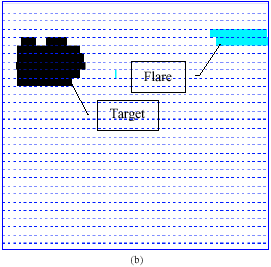
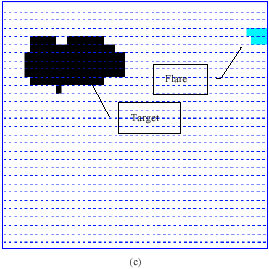
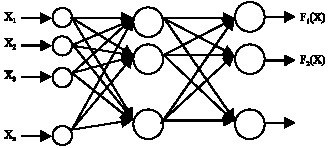
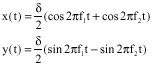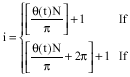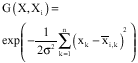Research Article
Feature Extraction and Classification of Objects in the Rosette Pattern Using Component Analysis and Neural Network
Department of Electrical Engineering, Iran University of Science and Technology, Narmak, 16846, Tehran, Iran
Shahriar Baradaran Shokouhi
Department of Electrical Engineering, Iran University of Science and Technology, Narmak, 16846, Tehran, Iran