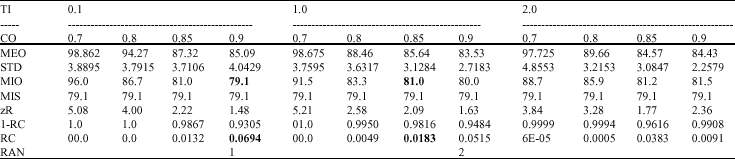
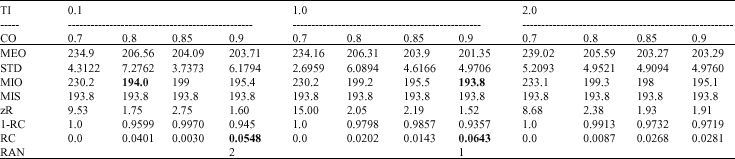
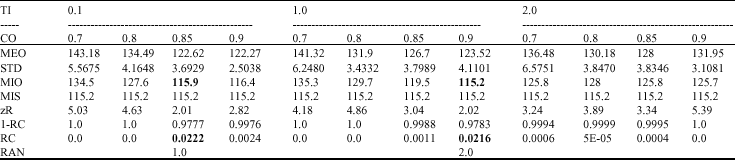
Research Article
A New Approach in Airport Capacity Enhancement Based on Integrated Runway Assignment and Operations Planning Model
Tarbiat Modares University, Tehran, Iran
I.N. Kamal Abadi
Tarbiat Modares University, Tehran, Iran
A.A. Kordani
Tarbiat Modares University, Tehran, Iran
E.A. Gangraj
Tarbiat Modares University, Tehran, Iran