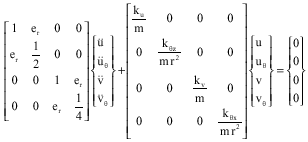
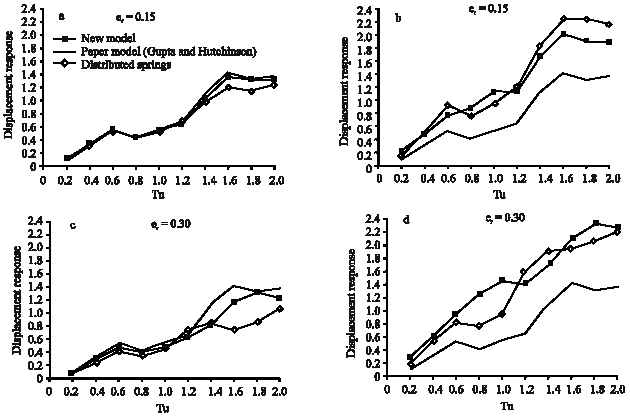
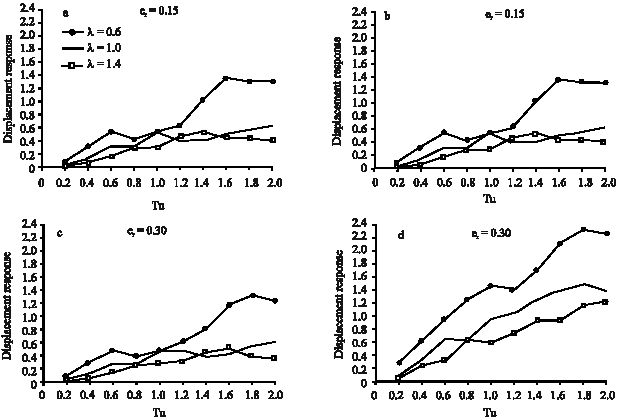
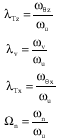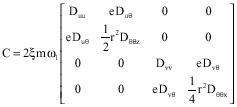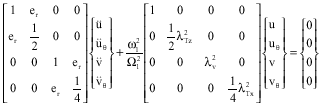Research Article
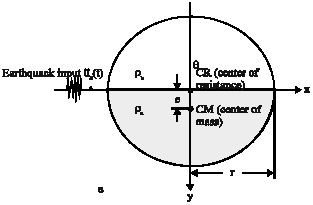
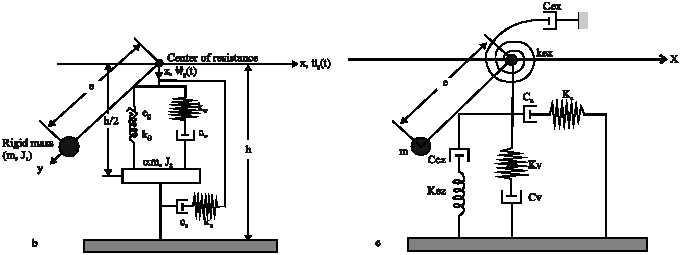
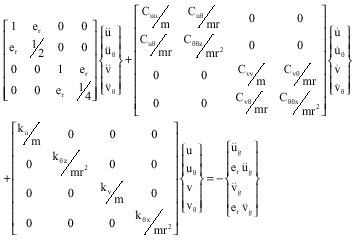
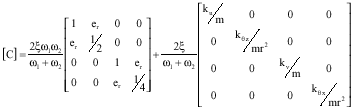
The Effect of Vertical Component of Earthquake on Seismic Response of Torsionally Coupled Systems
Structure and Earthquake Group in Science and Research Branch, The Islamic Azad University, Iran
A.S. Moghadam
Structural Engineering Research Center, The International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran
M. Hosseini
Structural Engineering Research Center, The International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran