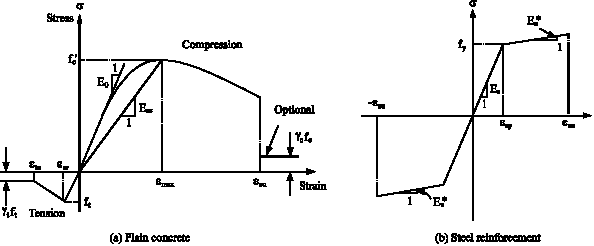
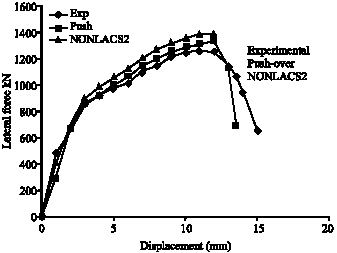
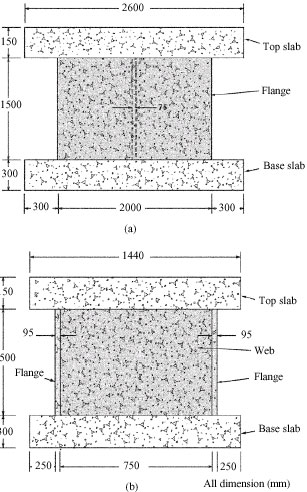
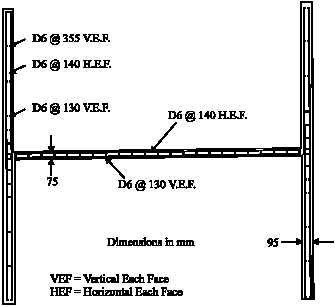
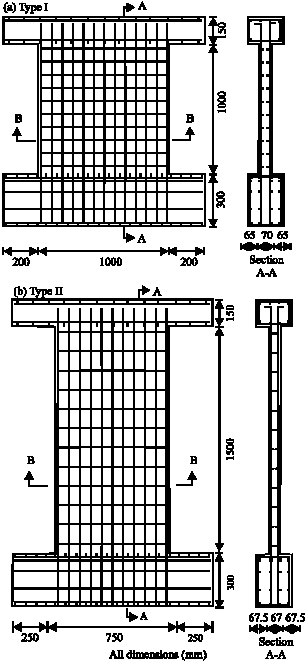
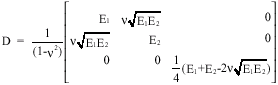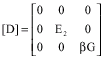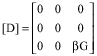Research Article
Nonlinear Analysis of RC Flanged Shear Walls Considering Tension-Stiffening Effect
Department of Civil Engineering, Faculty of Engineering, Semnan University, Semnan, Iran
Ali Kheyroddin
Department of Civil Engineering, Faculty of Engineering, Semnan University, Semnan, Iran