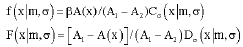Research Article
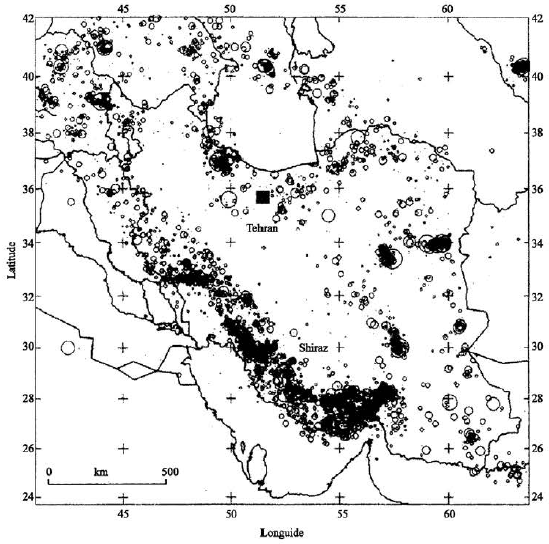
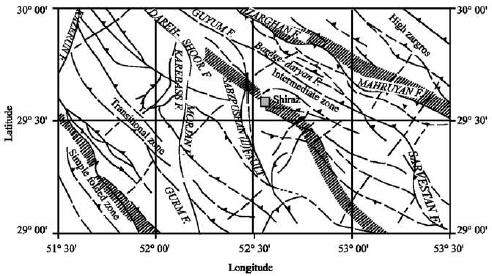
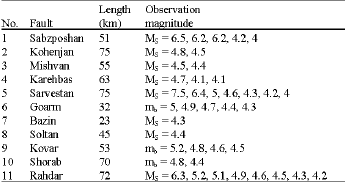
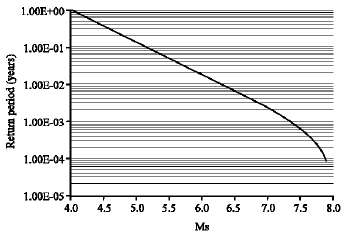
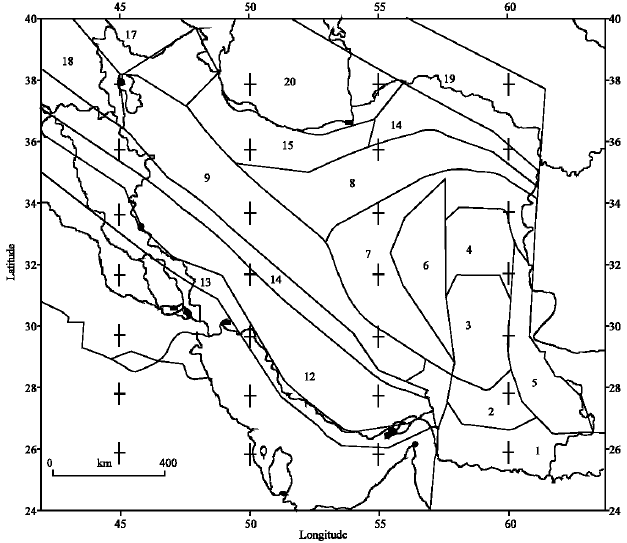
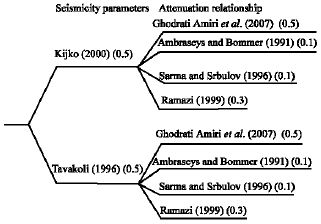
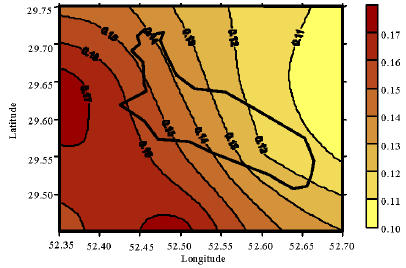
Seismic Hazard Assessment of Shiraz, Iran
1Center of Excellence for Fundamental Studies in Structural Engineering, College of Civil Engineering, Iran University of Science and Technology, P.O. Box 16765-163, Narmak, Tehran 16846, Iran
H.R. Razeghi
2College of Civil Engineering, Iran University of Science and Technology, Tehran, Iran
S.A. Razavian Amrei
2College of Civil Engineering, Iran University of Science and Technology, Tehran, Iran
H. Aalaee
3Faculty of Building and Housing, Building and Housing Research Center, Tehran, Iran
S.M. Rasouli
3Faculty of Building and Housing, Building and Housing Research Center, Tehran, Iran