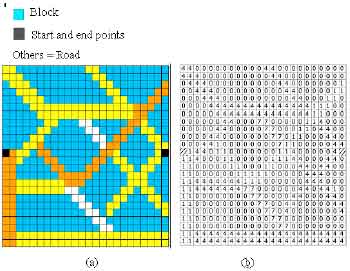
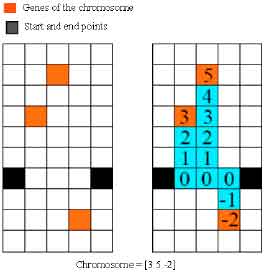
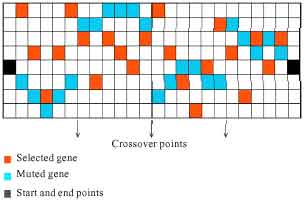
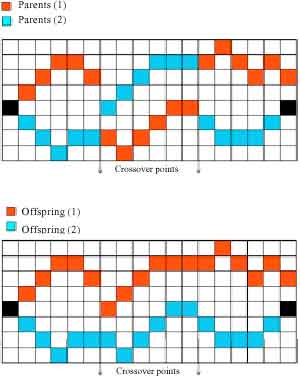
Research Article
Developing a Genetic Algorithm to Solve Shortest Path Problem on a Raster Data Model
Department of GIS Engineering, Faculty of Geomatics Engineering, K.N. Toosi University of Technology, ValiAsr Street, Mirdamad Cross, PC 19967-15433, Tehran, Iran
Ali A. Alesheikh
Department of GIS Engineering, Faculty of Geomatics Engineering, K.N. Toosi University of Technology, ValiAsr Street, Mirdamad Cross, PC 19967-15433, Tehran, Iran
E. Poorazizi
Department of GIS Engineering, Faculty of Geomatics Engineering, K.N. Toosi University of Technology, ValiAsr Street, Mirdamad Cross, PC 19967-15433, Tehran, Iran