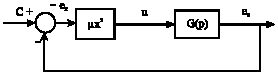
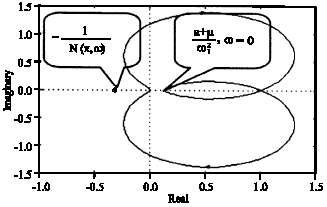
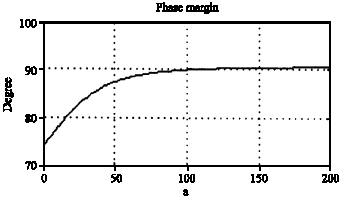
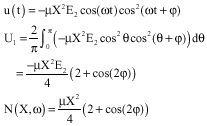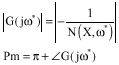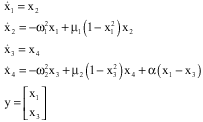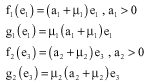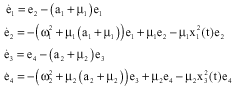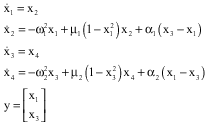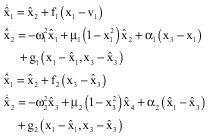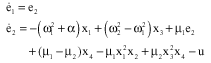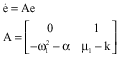Research Article
A State Observer and a Synchronization Method for Heart Pacemakers
Faculty of Engineering, Ferdowsi University of Mashhad, Iran
A. Azemi
College of Engineering, Penn State University, USA
M. Khademi
Faculty of Engineering, Ferdowsi University of Mashhad, Iran
M. Karimi-Ghartemani
Faculty of Electrical Engineering, Sharif University of Technology, Tehran, Iran