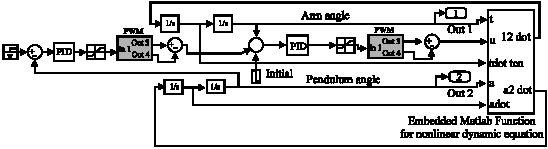
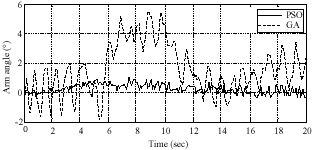
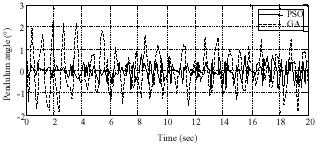
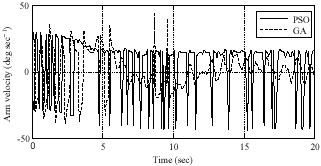
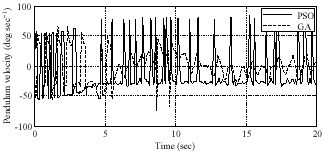
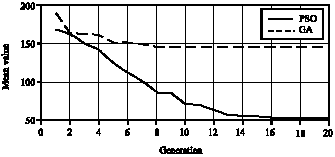
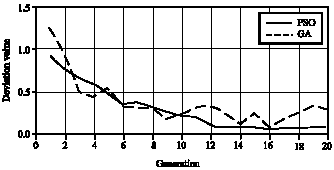
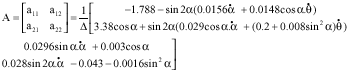Research Article
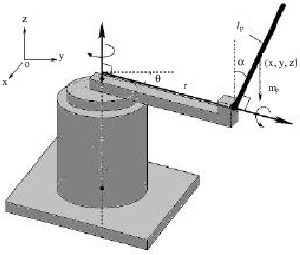
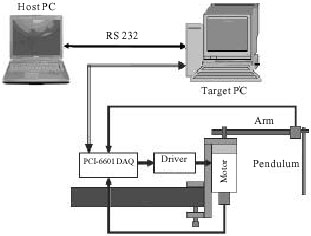
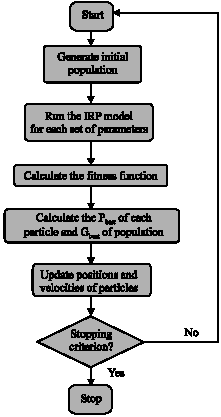
PSO-Based Controller Design for Rotary Inverted Pendulum System
Research Laboratory of Robotics, Department of Control Engineering,Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran
Saleh Mobayen
Research Laboratory of Robotics, Department of Control Engineering,Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran