Research Article
C-Fusion Frame
Department of Mathematics, University of Tabriz,Tabriz, Iran
R. Ahmadi
Department of Mathematics, University of Tabriz,Tabriz, Iran
INTRODUCTION
Throughout this study H will be a Hilbert space and Ĥ will be the collection of all closed subspace of H, respectively. Also, (X, μ) will be a measure space and v:X→[0, ∞) a measurable mapping such that v ≠ 0 a.e. We shall denote the unit closed ball of H by H1.
Frames was first introduced at (Duffin and Schaeffer, 1952) in the context of nonharmonik Fourier series. Outside of signal processing, frames did not seem to generate much interest until the ground breaking work of Daubechies et al. (1986). Since then the theory of frames began to be more widely studied. During the last 20 years the theory of frames has been growing rapidly, several new applications have been developed. For example, besides traditional application as signal processing, image processing, data compression and sampling theory, frames are now used to mitigate the effect of losses in pocket- based communication systems and hence to improve the robustness of data transmission (Casazza and Kovacevic, 2003) and to design high-rate constellation with full diversity in multiple-antenna code design (Hassibi et al., 2001). In Bolcskel et al. (1998), Benedetto et al. (2004) and Candes and Donoho (2004) some applications have been developed.
The fusion frames were considered by Casazza et al. (2000) in connection with distributed processing and are related to the construction of global frames. The fusion frame theory is in fact more delicate due to complicated relations between the structure of the sequence of weighted subspaces and the local frames in the subspaces and due to the extreme sensitivity with respect to changes of the weights.
In this study, we shall extend the fusion frames to their continuous versions in measure spaces.
PRELIMINARIES AND METHODS
This topics can be found by Christensen (2002).
Definition 1: Let {fi}iεI be sequence of members of H. We say that {fi}iεI is a frame for H if there exist 0 < A ≤ B < ∞ such that for all h ε H,
![]()
The constants A and B are called frame bounds. If A, B can be chosen so that A = B, we call this frame an A—tight frame and if A= B = 1 it is called a parseval frame. If we only have the upper bound, we call {fi}iεI a Bessel sequence. If {fi}iεI is a Bessel sequence then the following operators are bounded,

Definition 2: For a countable index set I, let {Wi}iεI be a family of closed subspace in H and let {vi}iεI be a family of weights, i.e., vi>0 for all i ε I. Then {(Wi,vi)}iεI is a fusion frame for H if there exist 0 < C ≤ D < ∞ such that for all h ε H:
![]()
where, ![]() is the orthogonal projection onto the subspace Wi. We call C and D the fusion frame bounds.
is the orthogonal projection onto the subspace Wi. We call C and D the fusion frame bounds.
The family {(Wi,vi)}iεI is called a C—tight fusion frame, if in above inequality the constants C and D can be chosen so that C = D, a parseval fusion frame provided C = D = 1 and an orthonormal fusion basis if H = ⊕iεIWi. If {(Wi,vi)}iεI possesses an upper fusion frame bound, but not necessarily a lower bound, we call it is a Bessel fusion sequence with Bessel fusion bound D.
The theory of frames has a continuous version as follows: Let (X, μ) be a measure space. Let f: X→H be weakly measurable (i.e., for all h ε H, the mapping x → < f(x), h > is measurable). Then f is called a continuous frame for H if there exist 0 < A ≤ B < ∞ such that, for all h ε H,
![]()
The following lemmas can be found in operator theory text books (Pedersen and Gert, 1989; Rudin, 1973, 1986; Sakai, 1998) which we shall use then in the text.
Lemma 1: Let u : H→K be a bounded operator. Then:
| • | ||u|| = ||u*|| and ||uu*|| = ||u||2. |
| • | Ru is closed, if and only if, Ru is closed. |
| • | u is subjective, if and only if, there exists c > 0 such that for each h ε H |
c||h||≤||u*(h)||
Lemma 2: Let u be a self-adjoint bounded operator on H. Let
![]()
and
![]()
Then, mu, Mu ε σ(u).
Theorem 1: Let u: K→H be a bounded operator with closed range Ru. Then there exists a bounded operator ux: H→K for which uuxf = f, F ε Ru.
Also, u*: H → K has closed range and (u*)† = (u†)*.
The operator ux is called the pseudo-inverse of u.
Theorem 2: Let u: K→H be a bounded surjective operator. Given y ε H, the equation ux = y has a unique solution of minimal norm, namely, x = uxy.
Now we introduce the concept of c-fusion frame and shall show some its properties.
Definition 4: Let F: X→Ĥ be such that for each h ε H, the mapping x a πF(X)(h) is measurable (i.e., F is weakly measurable). We say that (F, v) is a c-fusion frame for H if there exist 0 < A ≤ B < ∞ such that for all h ε H,
![]()
(F, v) is called a tight c-fusion frame for H if A, B can be chosen so that A = B and parseval if A = B = 1. If just the right hand inequality satisfies then we say that (F, v) is a Bessel c-fusion mapping for H.
Definition 3: Let F: X→Ĥ . Let L2(X, H, F) be the class of all measurable mapping f: X→H. such that for each x ε X and
f(x) ε F(x) and ![]()
It can be verified that L2(X, H, F) is a Hilbert space with inner product defined by:
![]()
Remark 1: For brevity, we shall denote L2(X, H, F) by L2(X, F). Let (F, v) be a Bessel c-fusion mapping, f ε L2(X, F) and h ε H. Then:
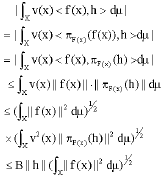
So we may define:
Definition 5: Let (F, v) be a Bessel c-fusion mapping for H. We define the c-fusion pre-frame operator TF: L2(X, F) by
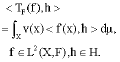
By the remark (5),
TF: L2(X, F)→H
is a bounded linear mapping. Its adjoint TF*: H→L2(X, F) will be called c-fusion analysis operator and SF = TF oTF* will be called c-fusion frame operator.
Remark 2: Let (F, v) be a Bessel c-fusion mapping for H. Then TF: L2(X, F)→H is indeed a vector-valued integral, which we shall denote by:
![]()
Where:

For each h ε H and f ε L2(X, F) we have:
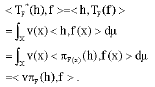
Hence for each h ε H, TF*(h) = vπF(h).
So TF* = vπF.
Therefore, SF: H → H is also a vector-valued integral which for each h ε H, we have
![]()
Definition 6: Let (F, v) and (G, v) are Bessel c-fusion mapping for H. We say (F, v) and (G, v) are weakly equal if TF* = TG*, which is equivalent with
vπF (h) = vπG (h), a.e.
for all h ε H Since, v≠ 0 a.e,. (F, v) and (G, v) are weakly equal if
πF (h) = πG (h), a.e.
for all h ε H.
Remark 3: Let TF = 0. Now, Let O: X→Ĥ be defined by:
O(x) = {0},
for almost all x ε X. Then (O, v) is a Bessel c-fusion mapping and TO = 0. Let h ε H. Since, vπF(h)εL2(X, F), so

Thus,
πF(x) (h) = 0, a.e.
Therefore,
πF (h) = πO (h), a.e.
Hence, (F, v) and (G, v) are weakly equal.
Definition 7: For each Bessel c-fusion mapping F for H, we shall denote
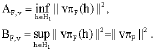
Remark 4: Let F is a Bessel c-fusion mapping for H. Since, for each h ε H.
<TFTF*(h), h > = ||vπF(h)||2,
AF,y and BF,y are optimal scalars which satisfy
AF,y≤TFTF*(h)≤ BF,y
So (F, v) is a c-fusion frame for H if and only if AF,y>0.
Lemma 3: Let (F, v) is a Bessel c-fusion mapping for H. Then F is c-fusion frame for H if and only if TF is surjective.
Proof: Let AF,y>0 Since, for each h ε H
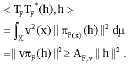
Therefore,
TF: L2(X, F)→H
is surjective.
Now let TF be surjective. Let
TFx: H → L2(X, F)
be its pseudo-inverse. Since, for each h ε H
![]()
so
![]()
Theorem 3: Let (F, v) be a Bessel c-fusion mapping for H, and K be a Hilbert space. Let u: H → K be a bounded bijective operator and (u oF, v) is a Bessel c-fusion mapping for K. Then:
| (i) | |
| (ii) | |
| (iii) | F is a c-fusion frame for H if and only if (u oF, v) is a c-fusion frame for K. |
Proof:
| (i) | It is straightforward. |
| (ii) | For each k ε K, we have |
| (iii) | It is clear from (ii) and Lemma 3. |

Hence
![]()
Lemma 4: Let (F, v) be a Bessel c-fusion mapping for H. Then the frame operator SF = TFTF* is invertible if and only if F is a c-fusion frame for H.
Proof: Let SF = TFTF* be invertible. We have
![]()
so, AF,y>0. Now let AF,y>0. So, by the Lemma 3, TF is surjective. Then there exist A>0 such that
![]()
Hence
![]()
Theorem 4: Let {Hi}iεI be a collection of Hilbert space and H = ⊕iHi. Let (F, v) be a Bessel c-fusion mapping for H such that for each i ε I there exist at most one x ε X such that F(x)⊆Hi. Let each finite subset of X be measurable. Then, for each h ε H
![]()
Proof: Let
![]()
Let {fn} be a sequence of members of K which tends to f ε H. Given ε>0, we can find N>0 such that ||fN—f||<ε There exists a finite Z⊆X such that for each finite Z⊆Y⊆Y,
![]()
We have
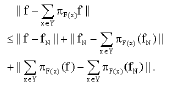
But

So, K is a closed subspace of H. Now, let h ε K⊥ Since, for each t ε X
![]()
![]() Since
Since
and AF,y>0. H = 0.
Theorem 5: Let (X, μ) and (Y, λ) be two σ—finite measure space and let f: XxY→H, F: X→Ĥ be weakly measurable mappings. Let for each x ε X, f(x,..): Y→F(x) be measurable and for every x ε F(x), f(x,.) is a continuous frame for H. Let

and let
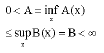
Then, (F, v) is a c-fusion frame for H if and only if
![]()
is a continuous frame for H.
Proof: For each h ε H we have

and the theorem is proved.
Theorem 6: Let (X, μ) be a σ—finite measure space and K be a Hilbert space. Let u: H → K be a bijective linear operator. Let F: X→Ĥ and be weakly measurable. Then, (F, v) is a c-fusion frame for H if and only if (u oF, v) is a c-fusion frame for K.
Proof: Let F be a c-fusion frame for H. Let (Y, λ) be a σ-finite measure space and let
f: XxY → H
be such that for each
x ε X, f(x,.):Y → F(x)
with
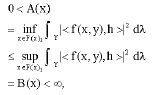
measurable and ![]() Choosing such mapping is always possible, because let
Choosing such mapping is always possible, because let ![]() be an orthonormal basis for F(x). We can suppose that
be an orthonormal basis for F(x). We can suppose that ![]() is pairwise disjoint (we can consider {x}xI). Let
is pairwise disjoint (we can consider {x}xI). Let ![]() and λ be the counting measure on Y. Then we can define f: XxY → H by
and λ be the counting measure on Y. Then we can define f: XxY → H by
![]()
and
f(x, i) = 0 otherwise
Then, for each x ε X
A(x) = B(x) = 1
By the Theorem 3
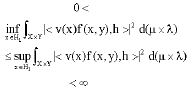
Then, and for each x ε X,
![]()
Since, u is surjective, there is C > 0 such that
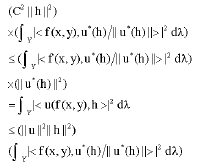
So,
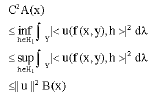
Similarly, we have

Therefore by the Theorem 3 be a c-fusion frame for (u oF, v). The proof of the converse is similar.
Theorem 7: Let (F, v) be a c-fusion frame for H. Let h ε H and SF = TFTF*. Then:
(i) We have the following retrieval formulas
![]()
and
![]()
(ii) In the retrieval formula
![]()
![]() has least norm among all of the retrieval formulas.
has least norm among all of the retrieval formulas.
(iii) For each h ε H,
![]()
Proof:
(i) Since (F, v) is a c-fusion frame, SF is an invertible operator. By the Theorem 4, we have
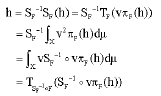
Also, we have
![]()
(ii) Let f ε L2(X, F) and
h = TF (f)
Thus, for each k ε H we have
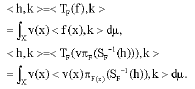
Therefore
![]()
So,
![]()
Hence
![]()
Since, F is a c-fusion frame,
![]()
But,
![]()
So,
![]()
and (ii) is proved.
(iii) Let f ε L2(X, F). Since, TFx is the unique solution of minimal norm of TF(f) = h so by
(ii),
![]()
Therefore,
![]()
Theorem 8: Let (F, v) and (G, v) be Bessel c-fusion mapping for H. Then the following assertions are equivalent:
(i) For each h ε H,
![]()
(ii) For each h ε H,
![]()
(iii) For each h , k ε H,
![]()
(iv) For each h ε H,
![]()
(v) For each orthonormal bases
{ei}iεI and {λj}jεJ
for H we have
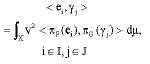
(iv) For each orthonormal bases {ei}iεI for H and i ε I,
![]()
Proof: (i) → (ii) Let h, k ε H. We have
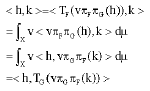
Hence, ![]()
(ii) → (iii) It is evident by the proof of (i) → (ii).
(iii) → (i) For each h, k ε H, we have
![]()
Thus ![]()
(iv) → (i) Let L: H → H be defined by
![]()
It clear that L is linear. Since
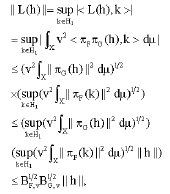
that, L ε B(H). For each h ε H, we have
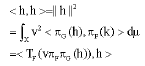
Hence, for each h ε H,
![]()
(iii) → (iv) is evident.
(v) → (iii) We have
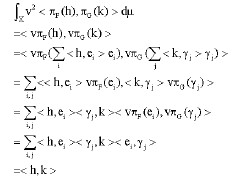
(vi) → (v) it is similar with the proof of (v) → (iii).