Research Article
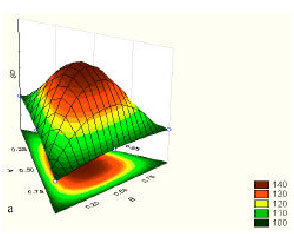
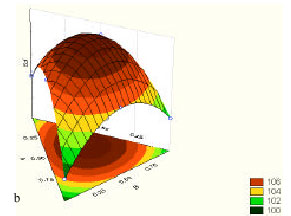
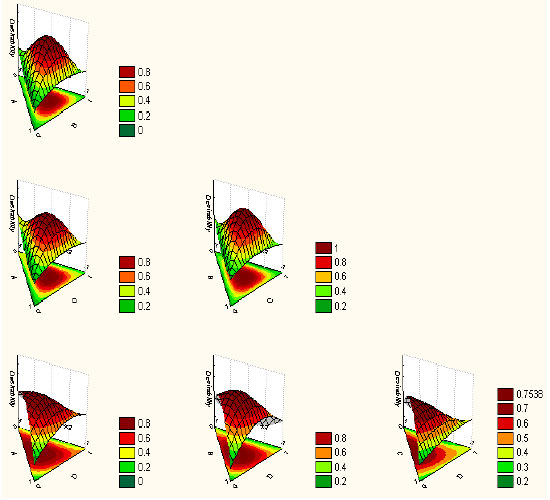
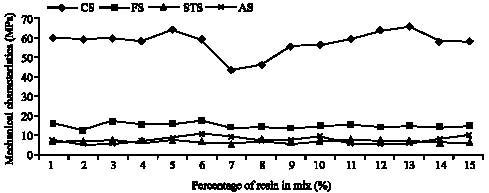
Mechanical Characteristics Investigation of Polymer Concrete Using Mixture Design of Experiments and Response Surface Method
Department of Concrete, Material, Technology and Organization, Technical University Gh. Asachi, Iasi, B-dul Mangeron 43, Iasi 700050, Romania
Daniel Lepadatu
Department of Civil Engineering, Technical University Gh. Asachi, Iasi, B-dul Mangeron 43, Iasi 700050, Romania