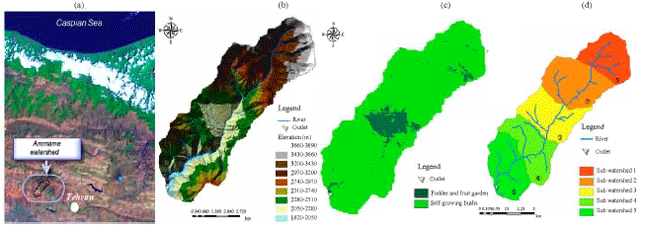
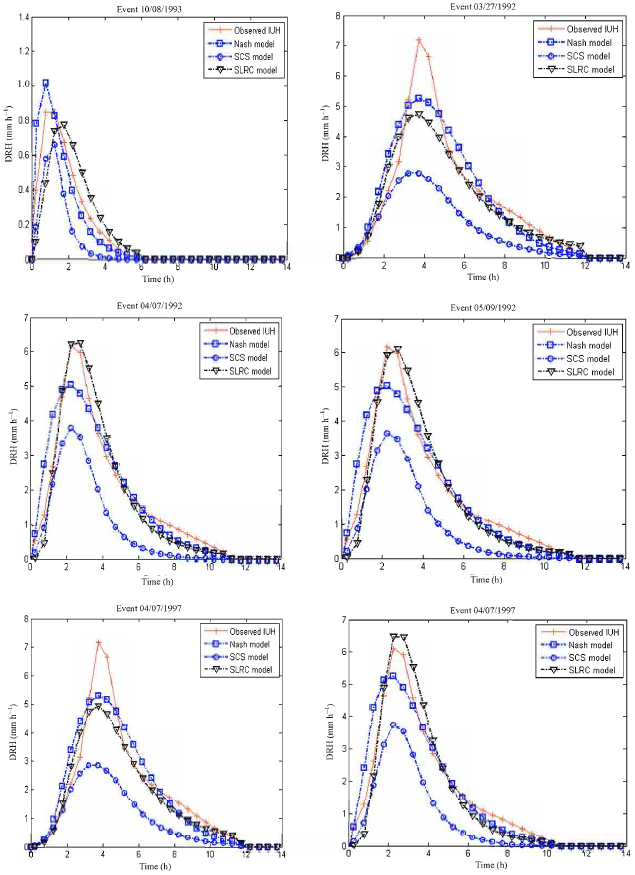
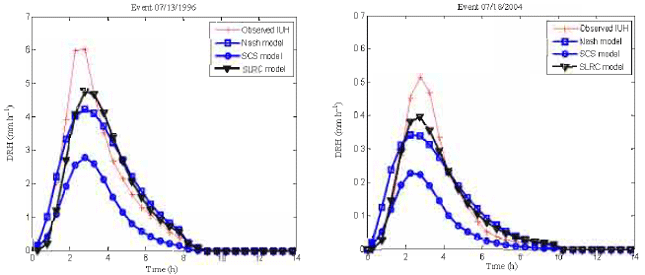
Research Article
Geomorphological Runoff Routing Modeling Based on Linear Reservoirs Cascade
Faculty of Civil Engineering, University of Tabriz, Tabriz, Iran
V.P. Singh
Faculty of Biological and Agricultural Engineering, Texas A and M University, Texas, USA
M.T. Alami
Faculty of Civil Engineering, University of Tabriz, Tabriz, Iran
H. Delafroz
Faculty of Civil Engineering, University of Tabriz, Tabriz, Iran