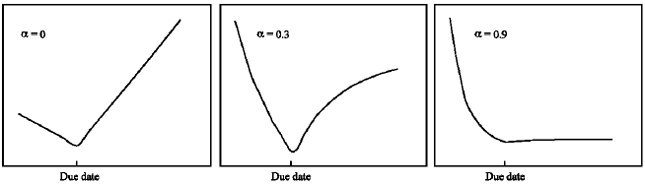
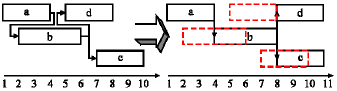
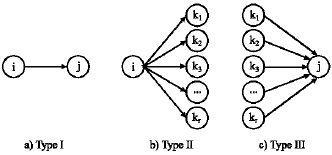
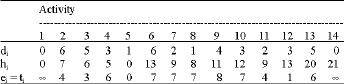
Research Article
An Algorithm for the Weighted Earliness-Tardiness Unconstrained Project Scheduling Problem
Department of Industrial Engineering, Sharif University of Technology,P.O. Box 11365-9414, Tehran, Iran
Shahram Shadrokh
Department of Industrial Engineering, Sharif University of Technology,P.O. Box 11365-9414, Tehran, Iran