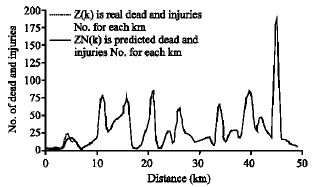
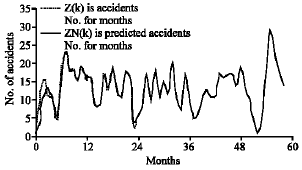
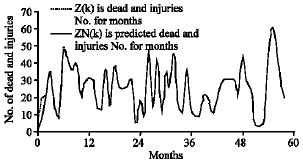
Research Article
Neural Networks Based Modelling of Traffic Accidents in Interurban Rural Highways, Duzce Sampling
Department of Construction, Faculty of Technical Education, D�zce �niversity, Konuralp, D�zce, Turkey
Recep Demirci
2Department of Electric, Faculty of Technical Education, D�zce �niversity, Konuralp, D�zce, Turkey